Аналитический метод решенияВ качестве аналитического метода наиболее распространен метод Гомори, который используется для случая n независимых переменных. Алгоритм решения по этому методу складывается из следующих этапов: 1. Решают задачу симплекс-методом без учета условий целочисленности.
где x1 –xm – базисные переменные, xm+1 –xn – свободные переменные, x, …, β,...,γ – свободные члены. Оптимальное решение будет В оптимальном решении из нецелых решений выбирают решение с наименьшей целой частью (пусть это будет
где { 3. Правильное отсечение приводят к каноническому виду введением дополнительной неотрицательной целочисленной переменной х n+1 по формуле: {- и включают новое уравнение в исходную систему ограничений. 4. Решают задачу симплекс-методом. Если не получается целочисленного значения, то вновь возвращаются к пункту 2.
1 этап. Исходную ЭММ приводят к каноническому виду посредством введения переменных x3 и x4, которые выбираются в качестве базисных. Преобразовывают задачу к задаче на min. max f (
x 1+3 x 2+ x 4=10,
x j min f ( f ( Решают пример обычным способом. Таблица 4.1 Исходная таблица
Таблица 4.2
|
2. Пусть на последнем шаге получены уравнения.
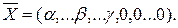
). Формулируют правильное отсечение по формуле:
{- 
{ 
}= 
.
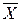)=2 x 1+4 x 2,
2 x 1+ x 2+ x 3= 
,
x 3
