Вероятность гипотез. Формулы Бейеса

Пусть событие А может наступить при условии появления одного из несовместных событий В₁, В₂,..., В_n, образующих полную группу. Поскольку заранее не известно, какое из этих событий наступит, их называют гипотезами. Вероятность появления события А определяется по формуле полной вероятности:

Р(А) = Р(В₁)Р_B1(А)+Р(В₂)Р_B2(А)+...+Р(В_n)Р_Bn(А). (*)

Допустим, что произведено испытание, в результате которого появилось событие А. Поставим своей задачей определить, как изменились (в связи с тем, что событие А уже наступило) вероятности гипотез. Другими словами, будем искать условные вероятности

Р_A(В₁), Р_A(В₂),.... Р_A(В_n).

Найдем сначала условную вероятность Р_A(В₁). По теореме умножения имеем

Р(АВ₁)=Р(А)Р_A(В₁)=Р(В₁)P_B1(А).

Отсюда

.

Заменив здесь Р(А) по формуле (*), получим

.

Аналогично выводятся формулы, определяющие условные вероятности остальных гипотез, т. е. условная вероятность любой гипотезы Вi (i=1, 2,..., n) может быть вычислена по формуле

.

Полученные формулы называют формулами Бейеса (по имени английского математика, который их вывел; опубликованы в 1764 г.). Формулы. Бейеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.

Пример. Детали, изготовляемые цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Вероятность того, что деталь попадает к первому контролеру, равна 0,6, а ко второму - 0,4. Вероятность того, что годная деталь будет признана стандартной первым контролером, равна 0,94, а вторым - 0,98. Годная деталь при проверке была признана стандартной. Найти вероятность того, что эту деталь проверил первый контролер.

Решение. Обозначим через А событие, состоящее в том, что годная деталь признана стандартной. Можно сделать два предположения:

1) деталь проверил первый контролер (гипотеза В₁);

2) деталь проверил второй контролер (гипотеза В₂). Искомую вероятность того, что деталь проверил первый контролер, найдем по формуле Бейеса:

.

По условию задачи имеем:

Р(В₁)=0,6 (вероятность того, что деталь попадает к первому контролеру);

Р(В₂) = 0,4 (вероятность того, что деталь попадет ко второму контролеру);

Р_В1(A)=0,94 (вероятность того, что годная деталь будет признана первым контролером стандартной);

Р_В2(A)=0,98 (вероятность того, что годная деталь будет признана вторым контролером стандартной). Искомая вероятность

P_A(B₁)=(0,6·0,94)/(0,6·0,944+0,4·0,98)≈0,59.

Как видно, до испытания вероятность гипотезы В₁ равнялась 0,6, а после того, как стал известен результат испытания, вероятность этой гипотезы (точнее, условная вероятность) изменилась и стала равной 0,59. Таким образом, использование формулы Бейеса позволило переоценить вероятность рассматриваемой гипотезы.

Задание

Решить задачи 89, 90,91,92,93,94,95,98,99,104,105

 

 

 

Содержание отчета

5.1 Наименование и цель работы

5.2 Условия задач

5.3 Выполненное задание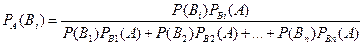