 Обе точки
Обе точки 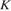 и
и  не могут лежать вне треугольника, поскольку в этом случае отрезок
не могут лежать вне треугольника, поскольку в этом случае отрезок  не может касаться вписанной окружности. Значит, по крайней мере одна из этих точек лежит на стороне треугольника.
не может касаться вписанной окружности. Значит, по крайней мере одна из этих точек лежит на стороне треугольника.
Пусть обе точки 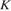 и
и  лежат на сторонах треугольника. Четырехугольник
лежат на сторонах треугольника. Четырехугольник  — вписанный, следовательно,
— вписанный, следовательно,

Значит, треугольник  подобен треугольнику
подобен треугольнику  , так как угол
, так как угол  — общий. Пусть коэффициент подобия равен
— общий. Пусть коэффициент подобия равен  , тогда
, тогда  ,
,  ,
, 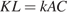 . Суммы противоположных сторон описанного четырехугольника
. Суммы противоположных сторон описанного четырехугольника  равны:
равны:


 Подставляя известные значения сторон, находим
Подставляя известные значения сторон, находим  . Следовательно,
. Следовательно,  .
.
Пусть точка 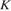 лежит на продолжении стороны
лежит на продолжении стороны  . Углы
. Углы  и
и  равны, поскольку опираются на одну дугу. Значит, треугольник
равны, поскольку опираются на одну дугу. Значит, треугольник  подобен треугольнику
подобен треугольнику  , так как угол
, так как угол  — общий. Более того, они описаны около одной и той же окружности. Следовательно, коэффициент подобия равен 1, то есть, треугольники
— общий. Более того, они описаны около одной и той же окружности. Следовательно, коэффициент подобия равен 1, то есть, треугольники  и
и  равны, поэтому
равны, поэтому  . Заметим, что
. Заметим, что  и точка
и точка 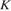 действительно лежит на продолжении стороны
действительно лежит на продолжении стороны  .
.
Если точка  лежит на продолжении стороны
лежит на продолжении стороны  , то
, то  , но, аналогично предыдущему случаю, получаем
, но, аналогично предыдущему случаю, получаем 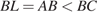 . Значит, этот случай не достигается.
. Значит, этот случай не достигается.
Ответ: 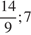 .
.
5. C 4. Точка  — центр правильного шестиугольника
— центр правильного шестиугольника  , в котором
, в котором  . Найдите радиус окружности, касающейся окружностей, описанных около треугольников
. Найдите радиус окружности, касающейся окружностей, описанных около треугольников  ,
,  И
И  .
.
Вариант № 3833168
1. C 4. Прямая, перпендикулярная гипотенузе прямоугольного треугольника, отсекает от него четырехугольник, в который можно вписать окружность. Найдите радиус окружности, если отрезок этой прямой, заключённый внутри треугольника, равен 12, а косинус острого угла равен  .
.

 Обе точки
Обе точки 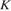 и
и  не могут лежать вне треугольника, поскольку в этом случае отрезок
не могут лежать вне треугольника, поскольку в этом случае отрезок  не может касаться вписанной окружности. Значит, по крайней мере одна из этих точек лежит на стороне треугольника.
не может касаться вписанной окружности. Значит, по крайней мере одна из этих точек лежит на стороне треугольника. — вписанный, следовательно,
— вписанный, следовательно,
 подобен треугольнику
подобен треугольнику  , так как угол
, так как угол  , тогда
, тогда  ,
,  ,
, 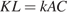 . Суммы противоположных сторон описанного четырехугольника
. Суммы противоположных сторон описанного четырехугольника 

 Подставляя известные значения сторон, находим
Подставляя известные значения сторон, находим  . Следовательно,
. Следовательно,  .
. . Углы
. Углы  и
и  равны, поскольку опираются на одну дугу. Значит, треугольник
равны, поскольку опираются на одну дугу. Значит, треугольник  . Заметим, что
. Заметим, что  и точка
и точка  , то
, то  , но, аналогично предыдущему случаю, получаем
, но, аналогично предыдущему случаю, получаем 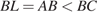 . Значит, этот случай не достигается.
. Значит, этот случай не достигается.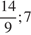 .
. — центр правильного шестиугольника
— центр правильного шестиугольника  , в котором
, в котором  . Найдите радиус окружности, касающейся окружностей, описанных около треугольников
. Найдите радиус окружности, касающейся окружностей, описанных около треугольников  ,
,  И
И  .
. .
.


