Решим первое неравенство.
 .
.
Неравенство заведомо выполняется, если правая часть отрицательнв, то есть, если 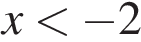
Если  то
то

Это верно только тогда, когда  .
.
Решение первого неравенства 
Решим второе неравенство:

Получаем  или
или 
Решением системы является общая часть решений обоих неравенств:
 или
или 
Ответ: 
5. C 3. Решите систему неравенств

Вариант № 3832815
1. C 4. Окружность, вписанная в треугольник  площадь которого равна
площадь которого равна 
касается средней линии, параллельной стороне  . Известно, что
. Известно, что  Найдите сторону
Найдите сторону  .
.
Решение.

Обозначим 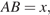
 пусть
пусть  − полупериметр треугольника
− полупериметр треугольника  Пусть
Пусть  и
и  − середины сторон
− середины сторон  и
и  соответственно. Тогда
соответственно. Тогда 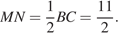
В трапеции  вписана окружность, поэтому
вписана окружность, поэтому

значит,


По формуле Герона:


Отсюда находим, что  или
или 
Ответ:  или
или  .
.
2. C 4. Площадь трапеции  равна 810. Диагонали пересекаются в точке
равна 810. Диагонали пересекаются в точке  Отрезки, соединяющие середину
Отрезки, соединяющие середину  основания
основания  с вершинами
с вершинами  и
и 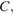 пересекаются с диагоналями трапеции в точках
пересекаются с диагоналями трапеции в точках  и
и  Найдите площадь треугольника
Найдите площадь треугольника  если одно из оснований трапеции вдвое больше другого.
если одно из оснований трапеции вдвое больше другого.
Решение.

Пусть  (рис. 1). Четырехугольники
(рис. 1). Четырехугольники  и
и  — параллелограммы, поэтому
— параллелограммы, поэтому  и
и  — середины
— середины  и
и  значит,
значит,  и
и  — медианы треугольника
— медианы треугольника  Пусть
Пусть  — высота трапеции. Положим
— высота трапеции. Положим  Тогда
Тогда

а  т. к.
т. к.  — точка пересечения медиан треугольника
— точка пересечения медиан треугольника 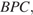 поэтому
поэтому

Аналогично,  значит, треугольник
значит, треугольник  подобен треугольнику
подобен треугольнику  с коэффициентом
с коэффициентом  Заметим, что поскольку треугольники AOD и BOC подобны с коэффициентом 2, высота треугольника AOD вдвое больше высоты треугольника BOC и составляет две трети высоты трапеции. Имеем:
Заметим, что поскольку треугольники AOD и BOC подобны с коэффициентом 2, высота треугольника AOD вдвое больше высоты треугольника BOC и составляет две трети высоты трапеции. Имеем:

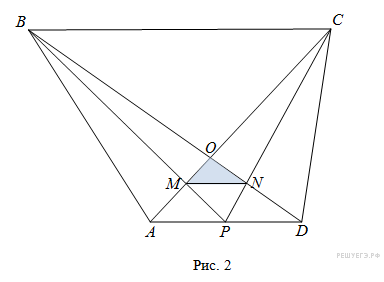
Рассмотрим случай, когда  (рис. 2) Пусть
(рис. 2) Пусть  — высота трапеции. Положим
— высота трапеции. Положим  Тогда
Тогда 
Треугольник  подобен треугольнику
подобен треугольнику  с коэффициентом
с коэффициентом  , а треугольник
, а треугольник  – треугольнику
– треугольнику  с коэффициентом
с коэффициентом 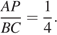 Тогда
Тогда

значит,  Аналогично,
Аналогично,  Следовательно,
Следовательно,
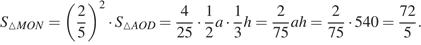
Ответ:  или
или 
3. C 4. Четырехугольник  описан около окружности и вписан в другую окружность. Прямые
описан около окружности и вписан в другую окружность. Прямые 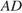 и
и  пересекаются в точке
пересекаются в точке  Найдите периметр треугольника
Найдите периметр треугольника  если известно, что
если известно, что  и
и 

 .
.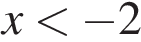
 то
то
 .
.

 или
или 



 площадь которого равна
площадь которого равна 
 . Известно, что
. Известно, что  Найдите сторону
Найдите сторону  .
.
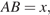
 пусть
пусть  − полупериметр треугольника
− полупериметр треугольника  Пусть
Пусть  и
и  − середины сторон
− середины сторон  и
и  соответственно. Тогда
соответственно. Тогда 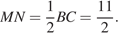
 вписана окружность, поэтому
вписана окружность, поэтому




 или
или 
 или
или  .
. равна 810. Диагонали пересекаются в точке
равна 810. Диагонали пересекаются в точке  Отрезки, соединяющие середину
Отрезки, соединяющие середину  основания
основания  с вершинами
с вершинами  и
и 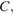 пересекаются с диагоналями трапеции в точках
пересекаются с диагоналями трапеции в точках  Найдите площадь треугольника
Найдите площадь треугольника  если одно из оснований трапеции вдвое больше другого.
если одно из оснований трапеции вдвое больше другого.
 (рис. 1). Четырехугольники
(рис. 1). Четырехугольники  и
и  — параллелограммы, поэтому
— параллелограммы, поэтому  и
и  значит,
значит,  и
и  — медианы треугольника
— медианы треугольника  Пусть
Пусть  — высота трапеции. Положим
— высота трапеции. Положим  Тогда
Тогда
 т. к.
т. к.  — точка пересечения медиан треугольника
— точка пересечения медиан треугольника 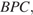 поэтому
поэтому
 значит, треугольник
значит, треугольник  подобен треугольнику
подобен треугольнику  с коэффициентом
с коэффициентом  Заметим, что поскольку треугольники AOD и BOC подобны с коэффициентом 2, высота треугольника AOD вдвое больше высоты треугольника BOC и составляет две трети высоты трапеции. Имеем:
Заметим, что поскольку треугольники AOD и BOC подобны с коэффициентом 2, высота треугольника AOD вдвое больше высоты треугольника BOC и составляет две трети высоты трапеции. Имеем:

 (рис. 2) Пусть
(рис. 2) Пусть  Тогда
Тогда 
 с коэффициентом
с коэффициентом  , а треугольник
, а треугольник  – треугольнику
– треугольнику  с коэффициентом
с коэффициентом 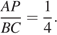 Тогда
Тогда
 Аналогично,
Аналогично,  Следовательно,
Следовательно,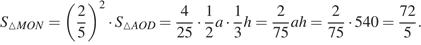
 или
или 
 описан около окружности и вписан в другую окружность. Прямые
описан около окружности и вписан в другую окружность. Прямые 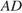 и
и  пересекаются в точке
пересекаются в точке  Найдите периметр треугольника
Найдите периметр треугольника  если известно, что
если известно, что  и
и 



