Предельный признак сравнения числовых положительных рядов
Предельный признак сравнения:Рассмотрим два положительных числовых ряда Важные примечания: 1) Если речь идёт о двух сходящихся рядах, то предел может быть равен и нулю (но не бесконечности). 2) Если речь идёт о двух расходящихся рядах, то предел может быть равен и бесконечности (но не нулю). Когда применяется предельный признак сравнения? Предельный признак сравнения применяется тогда, когда «начинкой» ряда у нас являются многочлены. Либо один многочлен в знаменателе, либо многочлены и в числители и в знаменателе. Один или оба многочлена также могут находиться под корнем. Сразу рассмотрим пример, для которого не сработал только что рассмотренный признак сравнения. Пример 10 Исследовать ряд на сходимость Сравним данный ряд со сходящимся рядом
Почему для сравнения был выбран именно ряд Примечание: когда мы используем предельный признак сравнения, не имеет значения, в каком порядке составлять отношение общих членов, в рассмотренном примере отношение можно было составить наоборот: Предельный признак сравнения применим почти для всех рядов, которые мы рассмотрели в предыдущем пункте: Пример 11 Исследовать ряд на сходимость
Что делать, если многочлены находятся и в знаменателе, и в числителе? Алгоритм решения почти такой же – нам нужно подобрать для сравнения подходящий ряд из «обоймы» обобщенного гармонического ряда. Пример 12 Исследовать ряд на сходимость Мы видим, что и в числителе и в знаменателе у нас многочлены, причем, в знаменателе многочлен находится под корнем. Подбираем ряд для сравнения 1) Сначала нужно найти старшую степень знаменателя. Если бы не было корня, то, понятно, что старшая степень знаменателя равнялась бы четырем. Что делать, когда есть корень? Мысленно или на черновике отбрасываем все члены, кроме старшего: 2) Выясняем старшую степень числителя. Очевидно, что она равна единице. 3) Из старшей степени знаменателя вычитаем старшую степень числителя: 2 – 1 = 1 Таким образом, наш ряд нужно сравнить с рядом По мере накопления опыта решения эти три пункта можно и нужно проводить мысленно. Сравним данный ряд с расходящимся гармоническим рядом (1) Составляем отношение общих членов. Пример 13 Исследовать ряд на сходимость Например, рассмотрим ряд
|

 и
и  . Если предел отношения общих членов этого ряда равен конечному, отличному от нуля числу
. Если предел отношения общих членов этого ряда равен конечному, отличному от нуля числу  :
:  , то оба ряда сходятся или расходятся одновременно.
, то оба ряда сходятся или расходятся одновременно.
 . Используем предельный признак сравнения. Известно, что ряд
. Используем предельный признак сравнения. Известно, что ряд  равен конечному, отличному от нуля числу, то будет доказано, что ряд
равен конечному, отличному от нуля числу, то будет доказано, что ряд  – тоже сходится.
– тоже сходится.
 – это не изменило бы сути дела.
– это не изменило бы сути дела.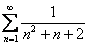 ,
,  ,
,  ,
,  .
. ,
,  ,
,  .
.

 .
. . Если есть константа, её тоже отбрасываем:
. Если есть константа, её тоже отбрасываем: 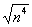 . Теперь извлекаем корень:
. Теперь извлекаем корень:  . Таким образом, старшая степень знаменателя равна двум.
. Таким образом, старшая степень знаменателя равна двум. , то есть, с расходящимся гармоническим рядом.
, то есть, с расходящимся гармоническим рядом. . Используем предельный признак сравнения:
. Используем предельный признак сравнения:
 устраняем стандартным способом деления числителя и знаменателя на «эн» в старшей степени.
устраняем стандартным способом деления числителя и знаменателя на «эн» в старшей степени. для внесения под корень:
для внесения под корень: 

 . Ага, 3 – 1 = 2, значит, ряд нужно сравнить со сходящимся рядом
. Ага, 3 – 1 = 2, значит, ряд нужно сравнить со сходящимся рядом 


