Если общий член ряда не стремится к нулю, то ряд расходится
Или короче: Если Докажем, что ряд из первого примера Необходимый признак сходимости ряда довольно часто встречается в практических заданиях: Пример 6 Исследовать ряд на сходимость когда старшие степени числителя и знаменателя равны, тогда предел равен конечному числу. Решаем:
Готово. Пример 7
Какие типы очевидно расходящихся рядов мы рассмотрели? Сразу понятно, что расходятся ряды вроде Почему признак называется необходимым? Потому-что, если общий член ряда стремится к нулю, ТО ЭТО ЕЩЕ НЕ ЗНАЧИТ, что ряд сходится. Или так: для того, чтобы ряд сходился, необходимо, чтобы его общий член стремился к нулю; но этого еще – не достаточно. Если общий член ряда стремится к нулю, то ряд может, как сходиться, так и расходиться! В таких случаях для решения примеров нужно использовать другие признаки. Знакомьтесь: Легко заметить, что Также следует запомнить понятие обобщенного гармонического ряда: Это элементарные факты из теории рядов, которые уже доказаны, и при решении какого-нибудь практического примера можно смело ссылаться, например, на расходимость ряда
|

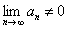 , то ряд расходится.
, то ряд расходится. расходится.
расходится.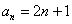
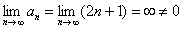
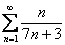
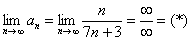

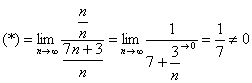
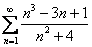
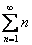 или
или 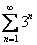 . Также расходятся ряды из примеров №№6,7: когда в числителе и знаменателе находятся многочлены, и старшая степень числителя больше либо равна старшей степени знаменателя. Во всех этих случаях при решении и оформлении примеров мы используем необходимый признак сходимости ряда.
. Также расходятся ряды из примеров №№6,7: когда в числителе и знаменателе находятся многочлены, и старшая степень числителя больше либо равна старшей степени знаменателя. Во всех этих случаях при решении и оформлении примеров мы используем необходимый признак сходимости ряда.
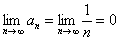 , НО. В теории математического анализа доказано, что гармонический ряд расходится.
, НО. В теории математического анализа доказано, что гармонический ряд расходится.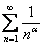
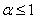 . Например, расходятся ряды
. Например, расходятся ряды 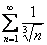 ,
, 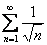 ,
, 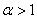 . Например, сходятся ряды
. Например, сходятся ряды  ,
,  ,
,  . Еще раз подчеркиваю, что почти во всех практических заданиях нам совершенно не важно, чему равна сумма, например, ряда
. Еще раз подчеркиваю, что почти во всех практических заданиях нам совершенно не важно, чему равна сумма, например, ряда 


