Существуют два признака сравнения, один из них я буду называть просто признаком сравнения, другой – предельным признаком сравнения.
Сначала рассмотрим признак сравнения. На практике он встречается довольно редко, но эта статья была бы неполной без данной информации.
Признак сравнения:Рассмотрим два положительных числовых ряда  и
и  . Если известно, что ряд
. Если известно, что ряд  – сходится, и выполнено неравенство
– сходится, и выполнено неравенство  (для
(для  ), то ряд
), то ряд  тоже сходится.
тоже сходится.
Иными словами: Из сходимости ряда с бОльшими членами следует сходимость ряда с меньшими членами.
Пример 8
Исследовать ряд на сходимость 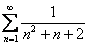
Заглядываем в «пачку» обобщенного гармонического ряда и находим похожий ряд:  . Из теории известно, что он сходится. Теперь нам нужно показать, что всех значений
. Из теории известно, что он сходится. Теперь нам нужно показать, что всех значений  справедливо неравенство
справедливо неравенство  .
.
Сравним исследуемый ряд со сходящимся рядом  . Используем признак сравнения. Для рассматриваемых рядов выполнено неравенство
. Используем признак сравнения. Для рассматриваемых рядов выполнено неравенство  , значит, по признаку сравнения исследуемый ряд сходится вместе с рядом
, значит, по признаку сравнения исследуемый ряд сходится вместе с рядом  .
.
В принципе, можно расписать и подробнее, указав, что неравенство выполняется для нескольких первых членов.
Проанализируем признак сравнения и решенный пример с неформальной точки зрения. Все-таки, почему ряд 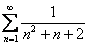 сходится? А вот почему. В теории доказано, что ряд
сходится? А вот почему. В теории доказано, что ряд  сходится, значит, он имеет некоторую конечную сумму
сходится, значит, он имеет некоторую конечную сумму  :
: 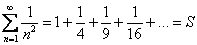 . Если все члены ряда
. Если все члены ряда 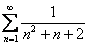 меньше соответствующих членов ряда
меньше соответствующих членов ряда  , то ясен пень, что сумма ряда
, то ясен пень, что сумма ряда 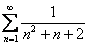 не может быть больше числа
не может быть больше числа  , и тем более, не может равняться бесконечности!
, и тем более, не может равняться бесконечности!
Аналогично можно доказать сходимость «похожих» рядов:  ,
,  ,
,  и т.д.
и т.д.
! Обратите внимание, что во всех случаях в знаменателях у нас находятся «плюсы». Если есть минусы, то рассматриваемый признак сравнения может не дать результата. Например, рассмотрим ряд  . Попробуйте аналогично сравнить его со сходящимся рядом
. Попробуйте аналогично сравнить его со сходящимся рядом 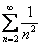 , выпишите несколько неравенств для первых членов. Вы увидите, что неравенство
, выпишите несколько неравенств для первых членов. Вы увидите, что неравенство  не выполняется и признак не дает нам ответа. Придется использовать другой признак, чтобы выяснить, сходится этот ряд или нет.
не выполняется и признак не дает нам ответа. Придется использовать другой признак, чтобы выяснить, сходится этот ряд или нет.
Пример 9
Исследовать ряд на сходимость 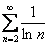
В примере я предлагаю самостоятельно рассмотреть вторую «зеркальную» часть теоремы: Если известно, что ряд  – расходится, и выполнено неравенство
– расходится, и выполнено неравенство  (для
(для  ), то ряд
), то ряд  тоже расходится.
тоже расходится.
Иными словами: Из расходимости ряда с меньшими членами следует расходимость ряда с бОльшими членами.
Что нужно сделать?
Нужно сравнить исследуемый ряд с расходящимся гармоническим рядом  : построить несколько неравенств и сделать вывод о справедливости неравенства
: построить несколько неравенств и сделать вывод о справедливости неравенства  .
.

 и
и  . Если известно, что ряд
. Если известно, что ряд  (для
(для  ), то ряд
), то ряд 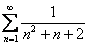
 . Из теории известно, что он сходится. Теперь нам нужно показать, что всех значений
. Из теории известно, что он сходится. Теперь нам нужно показать, что всех значений  .
. :
: 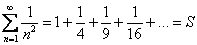 . Если все члены ряда
. Если все члены ряда  ,
,  ,
,  и т.д.
и т.д. . Попробуйте аналогично сравнить его со сходящимся рядом
. Попробуйте аналогично сравнить его со сходящимся рядом 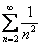 , выпишите несколько неравенств для первых членов. Вы увидите, что неравенство
, выпишите несколько неравенств для первых членов. Вы увидите, что неравенство 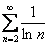
 (для
(для  : построить несколько неравенств и сделать вывод о справедливости неравенства
: построить несколько неравенств и сделать вывод о справедливости неравенства 


