Понятие числового положительного ряда
В общем виде положительный числовой ряд можно записать так:  .
.
Здесь:
 – математический значок суммы;
– математический значок суммы;
 – общий член ряда (запомните этот простой термин);
– общий член ряда (запомните этот простой термин);
 – переменная-«счётчик». Запись
– переменная-«счётчик». Запись  обозначает, что проводится суммирование от 1 до «плюс бесконечности», то есть, сначала у нас
обозначает, что проводится суммирование от 1 до «плюс бесконечности», то есть, сначала у нас  , затем
, затем  , потом
, потом  , и так далее – до бесконечности. Вместо переменной
, и так далее – до бесконечности. Вместо переменной  иногда используется переменная
иногда используется переменная  или
или  . Суммирование не обязательно начинается с единицы, в ряде случаев оно может начинаться с нуля
. Суммирование не обязательно начинается с единицы, в ряде случаев оно может начинаться с нуля  , с двойки
, с двойки  либо с любого натурального числа.
либо с любого натурального числа.
В соответствии с переменной-«счётчиком» любой ряд можно расписать развёрнуто:
 – и так далее, до бесконечности.
– и так далее, до бесконечности.
Будем считать, что ВСЕ слагаемые  – это неотрицательные ЧИСЛА. То есть, на данном уроке речь пойдет о положительных числовых рядах.
– это неотрицательные ЧИСЛА. То есть, на данном уроке речь пойдет о положительных числовых рядах.
Пример 1
Записать первые три члена ряда

Это уже, кстати, «боевое» задание – на практике довольно часто требуется записать несколько членов ряда.
Сначала  , тогда:
, тогда: 
Затем  , тогда:
, тогда: 
Потом  , тогда:
, тогда: 
Процесс можно продолжить до бесконечности, но по условию требовалось написать первые три члена ряда, поэтому записываем ответ: 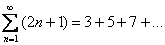
Сходимость числовых положительных рядов Необходимый признак сходимости ряда
Одной из ключевых задач теории числовых рядов является исследование ряда на сходимость. При этом возможны два случая:
1) Ряд  расходится. Это значит, что бесконечная сумма равна бесконечности:
расходится. Это значит, что бесконечная сумма равна бесконечности:  . Хороший пример расходящегося числового ряда встретился в начале урока:
. Хороший пример расходящегося числового ряда встретился в начале урока:  . Здесь совершенно очевидно, что каждый следующий член ряда – больше, чем предыдущий, поэтому
. Здесь совершенно очевидно, что каждый следующий член ряда – больше, чем предыдущий, поэтому  и, значит, ряд расходится. Чуть ниже мы рассмотрим более строгий математический критерий для данного примера.
и, значит, ряд расходится. Чуть ниже мы рассмотрим более строгий математический критерий для данного примера.
2) Ряд  сходится. Это значит, что бесконечная сумма равна некоторому конечному числу
сходится. Это значит, что бесконечная сумма равна некоторому конечному числу  :
:  . В качестве примера сходящегося числового ряда можно привести бесконечно убывающую геометрическую прогрессию, известную нам со школы:
. В качестве примера сходящегося числового ряда можно привести бесконечно убывающую геометрическую прогрессию, известную нам со школы:  . Сумму членов бесконечно убывающей геометрической прогрессии можно найти по формуле:
. Сумму членов бесконечно убывающей геометрической прогрессии можно найти по формуле: 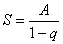 , где
, где  – первый член прогрессии,
– первый член прогрессии,  – основание прогрессии. В данном случае:
– основание прогрессии. В данном случае:  ,
, 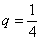 . Таким образом:
. Таким образом:  . Получено конечное число, значит, ряд
. Получено конечное число, значит, ряд  сходится, что и требовалось доказать.
сходится, что и требовалось доказать.
Существует несколько признаков сходимости ряда: необходимый признак сходимости ряда, признаки сравнения, признак Даламбера, признаки Коши, некоторые другие признаки. Когда какой признак применять? Это зависит от общего члена ряда  , образно говоря – от «начинки» ряда.
, образно говоря – от «начинки» ряда.

 .
. – математический значок суммы;
– математический значок суммы; – общий член ряда (запомните этот простой термин);
– общий член ряда (запомните этот простой термин); – переменная-«счётчик». Запись
– переменная-«счётчик». Запись  обозначает, что проводится суммирование от 1 до «плюс бесконечности», то есть, сначала у нас
обозначает, что проводится суммирование от 1 до «плюс бесконечности», то есть, сначала у нас  , затем
, затем  , потом
, потом  , и так далее – до бесконечности. Вместо переменной
, и так далее – до бесконечности. Вместо переменной  или
или  . Суммирование не обязательно начинается с единицы, в ряде случаев оно может начинаться с нуля
. Суммирование не обязательно начинается с единицы, в ряде случаев оно может начинаться с нуля  , с двойки
, с двойки  либо с любого натурального числа.
либо с любого натурального числа. – и так далее, до бесконечности.
– и так далее, до бесконечности. – это неотрицательные ЧИСЛА. То есть, на данном уроке речь пойдет о положительных числовых рядах.
– это неотрицательные ЧИСЛА. То есть, на данном уроке речь пойдет о положительных числовых рядах.



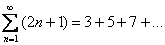
 расходится. Это значит, что бесконечная сумма равна бесконечности:
расходится. Это значит, что бесконечная сумма равна бесконечности:  . Хороший пример расходящегося числового ряда встретился в начале урока:
. Хороший пример расходящегося числового ряда встретился в начале урока:  . Здесь совершенно очевидно, что каждый следующий член ряда – больше, чем предыдущий, поэтому
. Здесь совершенно очевидно, что каждый следующий член ряда – больше, чем предыдущий, поэтому  и, значит, ряд расходится. Чуть ниже мы рассмотрим более строгий математический критерий для данного примера.
и, значит, ряд расходится. Чуть ниже мы рассмотрим более строгий математический критерий для данного примера. :
:  . В качестве примера сходящегося числового ряда можно привести бесконечно убывающую геометрическую прогрессию, известную нам со школы:
. В качестве примера сходящегося числового ряда можно привести бесконечно убывающую геометрическую прогрессию, известную нам со школы:  . Сумму членов бесконечно убывающей геометрической прогрессии можно найти по формуле:
. Сумму членов бесконечно убывающей геометрической прогрессии можно найти по формуле: 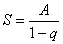 , где
, где  – первый член прогрессии,
– первый член прогрессии,  – основание прогрессии. В данном случае:
– основание прогрессии. В данном случае:  ,
, 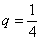 . Таким образом:
. Таким образом:  . Получено конечное число, значит, ряд
. Получено конечное число, значит, ряд  сходится, что и требовалось доказать.
сходится, что и требовалось доказать.


