Спектр биполярного П-образного сигнала
В качестве примера применения ряда Фурье рассмотрим частотный спектр биполярного П-образного сигнала (меандра), представленного на рис. 2.2. При показанном на рисунке выборе начала отсчета времени функция E (t) в интервале (– T / 2, T / 2) определяется следующим образом
Рис. 2.2
При t = 0 эта функция имеет разрыв первого рода. Следовательно, условия Дирихле выполняются. Поскольку функция E (t) является четной, то ряд Фурье будет содержать только косинусоиды с коэффициентами
Следовательно,
где w 1 – основная частота, а 3 w 1, 5 w 1, 7 w 1, … – частоты гармоник. Амплитуды основной гармонической составляющей и гармоник более высокого порядка равны
Рис. 2.3
Как и следовало ожидать, спектр рассматриваемого периодического процесса является линейчатым, состоящим из отдельных линий, соответствующих дискретным частотам w 1, 3 w 1, 5 w 1, 7 w 1 и т.д.; длины линий равны амплитудам гармоник
Рис. 2.4
Если начало отсчета времени сместить вправо (в положительном направлении по оси времени t) на величину T / 4, как показано на рис.2.3, то функция E (t) в интервале (– T / 2, T / 2) определится в виде
Эта функция становится нечетной, и ряд Фурье в этом случае будет содержать только синусоиды, причем, как и выше, коэффициент A 0 = 0, а коэффициенты
Так как
Видим, что в обоих случаях частоты гармоник и соответствующие им амплитуды одинаковы, спектр не зависит от положения начала отсчета времени. Если в разложении ограничиться только основной и двумя следующим гармониками, то точность такого представления функции E (t) составит примерно 91%.
[1] Отрицательной частоте в геометрическом представлении гармонических колебаний формально можно поставить в соответствие вращение вектора E в направлении, противоположном соответствующем положительной частоте, т.е. по часовой стрелке.
|


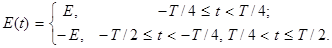



 .
. при нечетном m и Am = 0 при четном m. Как видим, при Bm = 0 коэффициенты Am совпадают с амплитудами Сm соответствующих гармоник. Ряд Фурье в этом случае запишется в виде
при нечетном m и Am = 0 при четном m. Как видим, при Bm = 0 коэффициенты Am совпадают с амплитудами Сm соответствующих гармоник. Ряд Фурье в этом случае запишется в виде
 ,
, ,
,  ,
,  , …,
, …,  Как видим, амплитуды гармоник быстро убывают с ростом номера m.
Как видим, амплитуды гармоник быстро убывают с ростом номера m.
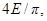

 и т.д. Заметим, что амплитуды гармоник убывают пропорционально
и т.д. Заметим, что амплитуды гармоник убывают пропорционально 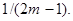 Спектр рассматриваемого сигнала показан на рис. 2.4.
Спектр рассматриваемого сигнала показан на рис. 2.4.

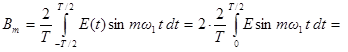
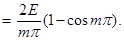
 , то все Bm = 0 при четном m и равны
, то все Bm = 0 при четном m и равны  при нечетном m. Ряд Фурье будет иметь вид
при нечетном m. Ряд Фурье будет иметь вид
 .
.


