ЧАСТОТНЫЙ СПЕКТР СИГНАЛОВ
Перцентиль – сотая доля объема всей совокупности людей, подвергающихся антропометрическим исследованиям. Каждая группа характеризуется определенными антропометрическими признаками. Если площадь, ограниченную кривой нормального распределения, и отражающую всю совокупность распределения разделить на сто равных частей, то получим 99 перцентилей. Они снабжаются порядковым номером. Первый перцентиль отсекает распределение частоты номинального значение антропометрического признака. Общие правила расчета параметров рабочего места: 1. Определяет характер контингента работающих. 2. Определяет объем (%) работающих, антропометрическим данным, которым должно соответствовать оборудование. 3. Выбирают антропометрический признак для основы расчета. 4. Выбирают границы объема обследуемой совокупности работающих. 5. При расчете параметров рабочего места используются пороговые значения антропометрических признаков. 6. Находят числовое выражение порогового значения антропометрического признака, характерное для выборочной совокупности. 7. Определяет базы отсчета. 8. Рассчитывают компоновочные параметры.
ЧАСТОТНЫЙ СПЕКТР СИГНАЛОВ
2.1. Общие представления о частотном спектре Как уже отмечалось, реальные световые волны никогда не бывают строго монохроматическими. Это обусловлено многими причинами и, прежде всего, самим механизмом излучения света. Свет, излучаемый реальными источниками, как будет показано в следующей главе, состоит из множества быстро сменяющих друг друга цугов (отрезков синусоид), амплитуды и начальные фазы которых изменяются беспорядочным образом; циклические частоты и длительности этих цугов также могут быть различными. Такой свет не является монохроматическим. Даже если выделить (например, с помощью светофильтра) цуги одинаковых частот, испускаемые одинаково возбужденными атомами, то и тогда из-за хаотичности изменения амплитуд и фаз цугов результирующее излучение не будет монохроматическим. Излучение не будет монохроматическим, как будет показано ниже, и вследствие ограниченности длительности и протяженности волновых цугов. Уже отмечалось также, что любое сложное немонохроматическое излучение можно представить в виде совокупности (в общем случае бесконечной) монохроматических волн. Такое представление называется спектральным разложением, или спектральным анализом (иногда это называют гармоническим анализом). Совокупность частот гармонических составляющих, входящих в состав сложного излучения, называют частотным спектром этого излучения. Спектр может быть как дискретным, состоящим из отдельных частот
w 1, w 2, w 3, …, w m, …, (2.1) так и непрерывным, когда частоты непрерывно заполняют некоторый интервал, называемый спектральным интервалом. Спектральный интервал может быть и бесконечным. Графически спектр изображают как распределение интенсивности излучения по частотам (или длинам волн). На рис. 2.1 показаны примеры дискретного (а) и непрерывного (б) спектров. С математической точки зрения замена немонохроматического излучения совокупностью монохроматических волн означает разложение функции, описывающей излучение, либо в ряд Фурье (если эта функция периодическая), либо в интеграл Фурье (если – непериодическая). Смысл спектрального разложения состоит в том, что ему соответствует реальный физический процесс: любой спектральный прибор производит фактическое разложение сложного излучения источника света на монохроматические составляющие, причем каждая такая составляющая дает в спектральном приборе отдельную линию, называемую спектральной линией.
а) б) Рис. 2.1
Предположим, что напряженность электрического поля излучения имеет определенное направление и зависит только от одной пространственной переменной z и от времени t: E = E (z, t). В соответствии с теоремой Фурье, ее можно представить в виде суперпозиции плоских монохроматических волн Если функция E (t) периодическая и удовлетворяет некоторым условиям, называемым условиями Дирихле, то согласно теореме Фурье ее можно разложить в ряд Фурье
Здесь
Формально суммирование в (2.2) производится по всем частотам, как положительным (которые только и имеют физический смысл), так и отрицательным[1]. При этом, поскольку функция E (t) вещественная, то должно выполняться условие
Здесь Спектр периодического процесса является дискретным, или линейчатым, так как состоит из отдельных линий – вертикальных отрезков, соответствующих дискретным частотам Подставляя в (2.2) соотношение (2.4), будем иметь
Используя формулу
вытекающую из формулы Эйлера, можно от комплексной формы ряда Фурье перейти к его тригонометрической форме
где Сm = 2 Для практических применений более удобной является следующая тригонометрическая форма ряда Фурье:
где A 0, Am, Bm – коэффициенты ряда Фурье, определяемые равенствами
В такой форме сигнал E (t) представляется в виде бесконечной суммы синусоидальных и косинусоидальных составляющих, причем Am – амплитуда m -ой косинусоидальной составляющей сигнала, Bm – амплитуда m -ой синусоидальной составляющей. Комплексные амплитуды Em и Если функция E (t) – четная, то функции Используя соотношения (2.2), (2.3) и учитывая свойство ортогональности гармонических функций с кратными частотами, для интенсивности сложного периодического излучения можно получить
I = Предполагается, что постоянная составляющая ряда равна нулю (в физических задачах это почти всегда имеет место). Отсюда следует, что интенсивность сложного периодического процесса равна сумме интенсивностей гармонических составляющих (гармоник), т.е. в энергетическом отношении отдельные спектральные составляющие сложного периодического процесса аддитивны. По виду огибающей величин Отметим важное свойство любого периодического процесса: его гармонические составляющие взаимно независимы. Поэтому при изменении или даже удалении из спектра любых гармоник амплитуды и фазы оставшихся гармоник не изменяются. Непериодический сигнал является частным случаем периодического сигнала, у которого период бесконечно велик:
Это выражение представляет непериодическую функцию в виде суммы (интеграла) гармонических колебаний с бесконечно малыми амплитудами. Чтобы такое представление было возможно, функция E (t) должна удовлетворять определенным требованиям (условиям Дирихле), в частности, функция E (t) должна быть абсолютно интегрируема, т.е. должно выполняться неравенство
В физических задачах условия Дирихле обычно выполняются. Согласно теореме Фурье, интеграл (2.6) можно обратить и найти
Здесь Интегралы (2.7) и (2.6) называют соответственно преобразованием Фурье и обратным преобразованием Фурье. Пределы интегрирования в (2.6) и (2.7) определяются областями существования функций E (t) и E (w) соответственно. Преобразование Фурье будем обозначать символом F{…}, а обратное преобразование Фурье – символом F – 1{…}. В этих обозначениях
E (w) = F{ E (t)}, E (t) = F – 1 { E (w)}. Функцию E (w) называют фурье-спектром, спектральной плотностью или фурье-образом функции E (t). В свою очередь функцию E (t) называют обратным (или инверсным) фурье-образом функции E (w) или ее прообразом. Время t и круговую частоту w называют сопряженными переменными преобразования Фурье. При w = 0 выражение (2.7) принимает вид
Эта величина равна площади, ограниченной кривой E (t). Аналогично из (2.6) при t = 0 получаем
Здесь правая часть представляет собой площадь, ограниченную кривой E (w). Полученные результаты являются частными случаями преобразований Фурье. Отметим здесь, что хотя функция E (t) и ее фурье-образ E (w) обозначаются одним и тем же символом E, это не означает, что функции E (t) и E (w) имеют одинаковый вид и получаются одна из другой простой заменой аргументов t на w (или w на t). Вид этих функций различен. При этом размерность величины E (w) есть В⋅с / м, размерностью же величины E (t) является В / м. Как видно из (2.7), функцию E (t) можно рассматривать как суперпозицию бесконечно большого числа гармонических составляющих всевозможных частот. Величина
E (w) = Модуль Если найти спектр поля E (t) по формуле (2.7), то, подставляя его в (2.6), получим исходное поле E (t). Таким образом, описания полей временными функциями и спектрами равноправны, и поэтому можно использовать ту или иную форму, исходя из простоты математического анализа. Полная энергия непериодического процесса пропорциональна интегралу
Изменив порядок интегрирования по w и t и используя выражение (2.7), будем иметь
где учтено, что
Из этого важного соотношения, известного как равенство Парсеваля, следует, что энергия непериодического сигнала равна сумме энергий всех его спектральных составляющих. Таким образом, энергия сигнала может быть найдена интегрированием либо во временной области, либо в частотной. Сказанное имеет место и для интенсивности излучения, так как I = Величина, пропорциональная Равенство Парсеваля позволяет определить практическую ширину спектра сигнала: D w = w в – w н, где w ви w н – соответственно верхняя и нижняя граничные частоты спектра, при которых величина спектральной плоскости энергии ниже некоторого заданного значения. Преобразования Фурье (обратное и прямое) часто бывает удобно выражать не через круговые частоты w, а через линейные частоты n. Выраженные через частоты n, эти преобразования имеют вид
(обратное преобразование Фурье),
(прямое преобразование Фурье). В таком виде прямое и обратное преобразования Фурье являются симметричными друг другу. Сопряженными переменными здесь являются время t и линейная частота n. Чтобы придать физическую конкретность полученным выше формулам, рассмотрим несколько примеров их применения.
2.2. Частотный спектр некоторых простых сигналов
|



 Положив в волновой функции E (z, t) переменную z = 0, получим напряженность поля как функцию только времени t: E (0, t) = = E (t). Эта функция описывает колебание электрического поля в точке z = 0. В этом случае рассматривается спектральное разложение колебательного процесса, создаваемого волной в точке z = 0. Разложение будет производиться по гармоническим функциям
Положив в волновой функции E (z, t) переменную z = 0, получим напряженность поля как функцию только времени t: E (0, t) = = E (t). Эта функция описывает колебание электрического поля в точке z = 0. В этом случае рассматривается спектральное разложение колебательного процесса, создаваемого волной в точке z = 0. Разложение будет производиться по гармоническим функциям 
 . (2.2)
. (2.2)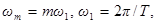 T – период функции E (t); число m принимает целые положительные и отрицательные значения. Берется вещественная часть ряда (2.2). Члены этого ряда называются гармониками соответственно первой или основной (при m = 1), второй (m = 2), третьей (m = 3) и т.д. Частота
T – период функции E (t); число m принимает целые положительные и отрицательные значения. Берется вещественная часть ряда (2.2). Члены этого ряда называются гармониками соответственно первой или основной (при m = 1), второй (m = 2), третьей (m = 3) и т.д. Частота  представляет собой частоту основной гармоники, поэтому ееназывают основной частотой периодического процесса. Число гармоник бесконечно велико. Комплексные коэффициенты Em ряда Фурье определяются интегралами
представляет собой частоту основной гармоники, поэтому ееназывают основной частотой периодического процесса. Число гармоник бесконечно велико. Комплексные коэффициенты Em ряда Фурье определяются интегралами
 (2.3)
(2.3) , где символ «* » обозначает комплексное сопряжение. Как комплексные величины коэффициенты Em можно представить в виде
, где символ «* » обозначает комплексное сопряжение. Как комплексные величины коэффициенты Em можно представить в виде (2.4)
(2.4) – амплитуда, а
– амплитуда, а  – начальная фаза m -ой гармоники. Две характеристики – амплитудная и фазовая, т.е. модули и аргументы комплексных коэффициентов ряда Фурье, полностью определяют структуру частотного спектра периодического колебания поля E (t). Совокупность величин
– начальная фаза m -ой гармоники. Две характеристики – амплитудная и фазовая, т.е. модули и аргументы комплексных коэффициентов ряда Фурье, полностью определяют структуру частотного спектра периодического колебания поля E (t). Совокупность величин  – спектром фаз. Спектр можно изобразить графически, откладывая по оси абсцисс частоты wm гармоник, а по оси ординат – их амплитуды
– спектром фаз. Спектр можно изобразить графически, откладывая по оси абсцисс частоты wm гармоник, а по оси ординат – их амплитуды  ) от их частоты.
) от их частоты. и т.д. Длины отрезков (в заданном масштабе) равны амплитудам соответствующих гармоник Em или их интенсивностям Im (рис. 2.1, а, если
и т.д. Длины отрезков (в заданном масштабе) равны амплитудам соответствующих гармоник Em или их интенсивностям Im (рис. 2.1, а, если  и т.д.).
и т.д.). .
.
 , (2.5)
, (2.5) за период. Запись ряда Фурье в таком виде удобна в тех случаях, когда нужно знать амплитуду и начальную фазу m -ой гармоники.
за период. Запись ряда Фурье в таком виде удобна в тех случаях, когда нужно знать амплитуду и начальную фазу m -ой гармоники. ,
, ;
; ;
;  .
. являются взаимно сопряженными комплексными величинами, так что равенство
являются взаимно сопряженными комплексными величинами, так что равенство  будут нечетными, и тогда все коэффициенты Bm = 0; если же E (t) – нечетная, то функции
будут нечетными, и тогда все коэффициенты Bm = 0; если же E (t) – нечетная, то функции  будут нечетными, и тогда все Am = 0. В первом случае ряд Фурье будет состоять из одних только косинусов, а во втором – из одних только синусов.
будут нечетными, и тогда все Am = 0. В первом случае ряд Фурье будет состоять из одних только косинусов, а во втором – из одних только синусов.


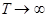 . Для непериодического процесса разложение функции E (t) по гармоническим составляющим представляется в виде интеграла Фурье
. Для непериодического процесса разложение функции E (t) по гармоническим составляющим представляется в виде интеграла Фурье . (2.6)
. (2.6) .
. . (2.7)
. (2.7) .
.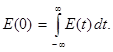
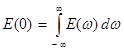 .
.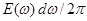 определяет вклад в E (t) гармонических составляющих из интервала частот (w, w + dw). Поэтому функция E (w) представляет собой спектральную плотность функции E (t). Как и в случае периодического поля E (t), она определяет распределение комплексных амплитуд гармоник по частотам, поэтому в общем случае она является комплексной. Комплексную функцию E (w) называют также комплексной амплитудой волны с частотой w (хотя на самом деле это – амплитуда, приходящаяся на единичный спектральный интервал). Как комплексную функцию ее можно записать в виде
определяет вклад в E (t) гармонических составляющих из интервала частот (w, w + dw). Поэтому функция E (w) представляет собой спектральную плотность функции E (t). Как и в случае периодического поля E (t), она определяет распределение комплексных амплитуд гармоник по частотам, поэтому в общем случае она является комплексной. Комплексную функцию E (w) называют также комплексной амплитудой волны с частотой w (хотя на самом деле это – амплитуда, приходящаяся на единичный спектральный интервал). Как комплексную функцию ее можно записать в виде exp [– ij (w)].
exp [– ij (w)]. – фазочастотную характеристику (ФЧХ) спектра непериодического процесса. Как видим, в случае непериодического процесса его спектр амплитуд является непрерывным.
– фазочастотную характеристику (ФЧХ) спектра непериодического процесса. Как видим, в случае непериодического процесса его спектр амплитуд является непрерывным. . Подставляя сюда выражение (2.6), получим
. Подставляя сюда выражение (2.6), получим


 . (2.8)
. (2.8) .
. , представляет собой энергию (и интенсивность) волны в интервале частот от w до w + + dw. Множитель
, представляет собой энергию (и интенсивность) волны в интервале частот от w до w + + dw. Множитель  в этом выражении имеет смысл энергии, приходящейся на единичный интервал частот, и может рассматриваться как спектральная плотность энергии. Эта величина характеризует энергетический спектр сигнала. Отметим, что энергия непериодического сигнала не зависит от фаз спектральных составляющих.
в этом выражении имеет смысл энергии, приходящейся на единичный интервал частот, и может рассматриваться как спектральная плотность энергии. Эта величина характеризует энергетический спектр сигнала. Отметим, что энергия непериодического сигнала не зависит от фаз спектральных составляющих. (2.9)
(2.9) (2.10)
(2.10)


