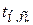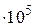Расчет сжатой железобетонной колонны с учетом симметричного коррозионного износа.
При выполнении задания учитывается влияние агрессивной газовоздушной среды. Математическая модель глубины
При Схема сжатой колонны с учетом влияния окружающей среды показана на рис. 1.
Рис.1. Схема колонны силовым и несиловым воздействием
Состав задания
1. Определить напряжения в начальный момент времени 2. Определить напряжения в моменты времени Построить графики напряжений 3. Определение времени исчерпания несущей способности 4. Определение первоначальной площади сечения колонны 5. Определить напряжения в бетоне для При вычислении напряжений может оказаться, что их уровень На диафрагме бетона показан секущий модуль, который определяется через коэффициент упруго-пластических деформаций
Здесь На рис. 2 показана диаграмма бетона
Рис. 2. Диаграмма бетона Через Через
Рис. 3. График
1. Определение напряжений в 1.1. Принимаем 1.2. Вычисляем сжимающую силу
1.3. Определение напряжений в предложении, что бетон работает в упругой стадии. 1.4. Вычисляем:
Напряжения в бетоне достаточно высокое
Необходимо учитывать нелинейную работу бетона. Вычисления выполняются итерационно. 1.5. Первая итерация: − коэффициент упруго-пластических деформаций
− секущий модуль
− − Напряжения 1.6. Вторая итерация − Уровень напряжений − Коэффициент
− − Секущий модуль
− Отношение модулей
− Напряжения в бетоне
− Напряжения в арматуре
1.7. Статическая проверка:
Вычислить:
Погрешность: Погрешность Расчет для времени Итоги расчета напряжений в Табл.1.
2. Определение напряжений в моменты времени
2.1. Определение напряжений в Вычислить: − Глубину коррозионного износа
Площадь двух коррозионных слоев
− Коэффициент коррозионного износа
Первая итерация Вычислить: − Необходимо расчет начать с какого-то значения − Вторая итерация Вычислить: − Уровень напряжений − − Секущий модуль − Отношение модулей
− Напряжения в бетоне
Погрешность Вычисление Напряжения в
Напряжение в арматуре
Статическая проверка
Погрешность Погрешность вполне допустимая. Особенность заключается в том, что со временем уменьшается рабочая площадь колонны
А коэффициент армирования увеличивается
Но увеличивается и Поэтому напряжения можно не пересчитывать. Об этом и говорит ничтожная погрешность. Итоги расчета напряжений в Табл. 2
2.2. Определение напряжений в Вычислить: − Глубину коррозионного износа
− Площадь двух коррозионных слоев
− Коэффициент коррозионного износа
− Напряжения в бетоне
Для вычисления первой итерации нужно задать значение
Вычислить: − Вторая итерация Вычислить: − Уровень напряжений − Коэффициент
− Секущий модуль − Коэффициент
Это значение отличается от
Оставляем результат первой итерации.
Статическая проверка
Погрешность Итоги расчета напряжений в Табл.3
2.3. Определение напряжений в Вычислить: − Глубину коррозионного износа
− Площадь двух коррозионных слоев
− Коэффициент коррозионного износа
− Напряжения в бетоне
Для вычисления первой итерации нужно задать значение
Вычислить: − Вторая итерация Вычислить: − Уровень напряжений − Коэффициент
− Секущий модуль − Коэффициент
Погрешность Вычисление
Напряжение в арматуре
Площадь бетона после коррозионного износа
Итоги расчета напряжений в Табл.4
2.4. Построение графиков
Изменение напряжений в бетоне и арматуре во времени при действии постоянной сжимающей силе и коррозии.
3. Определение времени исчерпания несущей способности
4. Определение первоначальной площади, которую нужно принять в
Откуда размер ребра колонны
5. Определение напряжений для времени
Напряжения Вывод: время эксплуатации Исходные данные Таблица
|

 коррозионного износа принимается в экспоненциальной форме
коррозионного износа принимается в экспоненциальной форме (1)
(1)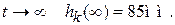 Показатели
Показатели  зависят от степени слабой, средне, сильно агрессивной среды принимает значения 30, 15, 7,5.
зависят от степени слабой, средне, сильно агрессивной среды принимает значения 30, 15, 7,5.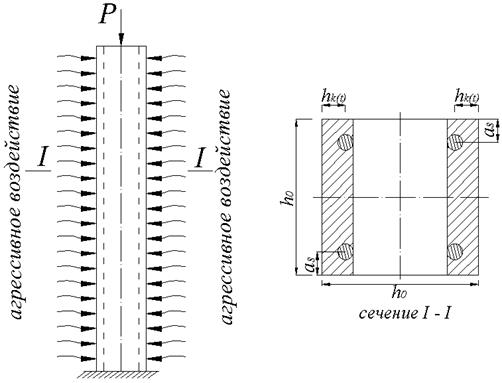
 МПа
МПа
 МПа
МПа
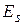 МПа
МПа
 см
см

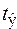 годы
годы

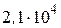
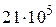
 до начала влияния окружающей среды.
до начала влияния окружающей среды.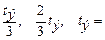 равного сроку эксплуатации здания с учетом коррозионного износа.
равного сроку эксплуатации здания с учетом коррозионного износа. и площади коррозионного износа.
и площади коррозионного износа. при достижении напряжений в бетоне прочности
при достижении напряжений в бетоне прочности 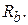
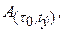 чтобы к окончанию срока службы здания напряжения в бетоне колонны достигли
чтобы к окончанию срока службы здания напряжения в бетоне колонны достигли 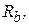 но не превзошли его.
но не превзошли его.
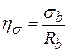 будет достаточно высоким. Тогда необходимо будет учитывать работу бетона, как нелинейно-упругого материала.
будет достаточно высоким. Тогда необходимо будет учитывать работу бетона, как нелинейно-упругого материала.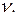 Этот коэффициент определяется по формуле (2) или графику рис. 3.
Этот коэффициент определяется по формуле (2) или графику рис. 3.
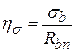 - уровень напряжений.
- уровень напряжений. и как определяются начальный модуль упругости и секущий.
и как определяются начальный модуль упругости и секущий.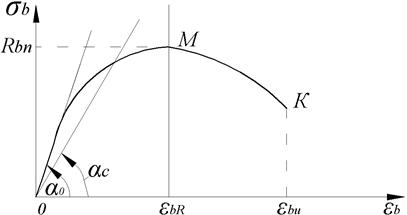

 - определяется
- определяется  - определяется секущий модуль
- определяется секущий модуль 

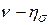


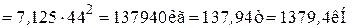



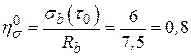



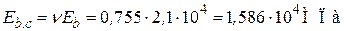





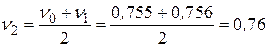





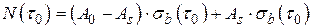
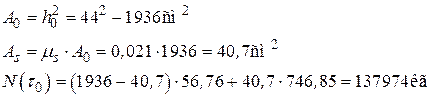

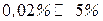 допустимая.
допустимая.

 МПа
МПа
 МПа
МПа










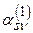 . Принимаем
. Принимаем  увеличим его на единицу.
увеличим его на единицу. 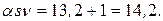
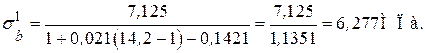
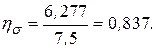


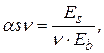
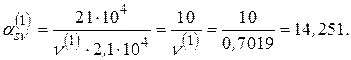

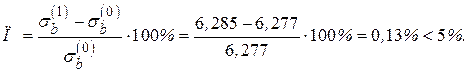
 закончено.
закончено.


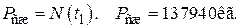



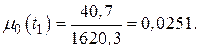
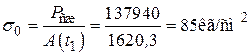
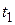 годы
годы
 см2
см2
 см2
см2
 МПа
МПа
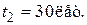

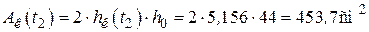


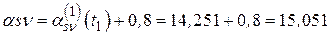
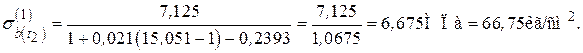
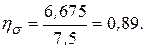



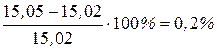
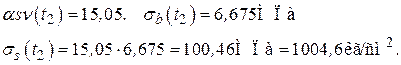
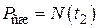


 годы
годы


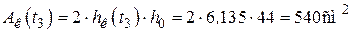

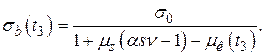

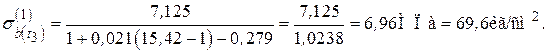



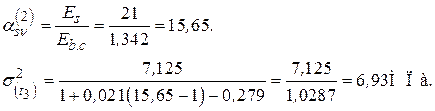

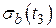 закончено
закончено
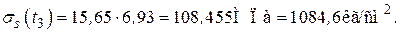

 превышает
превышает  на 0,09%.
на 0,09%.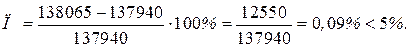

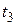 годы
годы

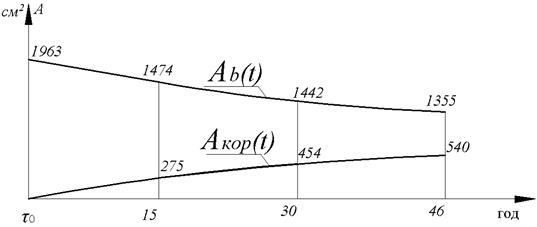
 − изменение рабочей площади бетона колонны
− изменение рабочей площади бетона колонны − изменение площади коррозионного износа
− изменение площади коррозионного износа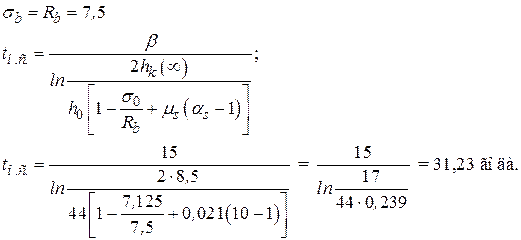
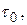 чтобы к концу времени эксплуатации колонна еще обладала несущей способностью.
чтобы к концу времени эксплуатации колонна еще обладала несущей способностью.


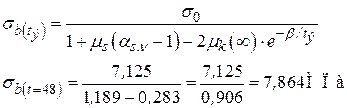

 должно быть меньше времени
должно быть меньше времени