Решение задач
1. Вариант 1. В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 3,6; 3,8; 4,3. Тогда несмещенная оценка дисперсии равна … · 0,13 · 0,065 · 3,9 · 0,7
Вариант 2.
Проведено пять измерений (без систематических ошибок) некоторой случайной величины (в мм): 2,1; 2,3;; 2,7; 2,9. Если несмещенная оценка математического ожидания равна 2,48, то равно … · 2,4 · 2,5 · 2,6 · 2,48
Вариант 3.
Проведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 8, 9, · 2,5 · 2,0 · 0 · 1,5
Вариант 4.
Проведено пять измерений (без систематических ошибок) некоторой случайной величины (в мм): 4,5; 5,2; 6,1; 7,8, 8,3. Тогда несмещенная оценка математического ожидания равна … · 6,38 · 6,42 · 6,1 · 6,4
Вариант 5.
В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 15; 18; 21; 24. Тогда выборочная дисперсия равна … · 11,25 · 19,5 · 15 · 21,25
2. Вариант 1.
Из генеральной совокупности извлечена выборка объема
Тогда выборочное среднее квадратическое отклонение равно … · · · 10,46 ·
Вариант 2.
По выборке объема · 2,0 · 4,0 · 3,24 · 1,8
Вариант 3.
Из генеральной совокупности извлечена выборка объема
Тогда несмещенная оценка математического ожидания равна …
· 13,14 · 13,0 · 13,34 · 13,2
3. Вариант 1.
Если все варианты
· увеличится в четыре раза · увеличится в два раза · не изменится · увеличится на четыре единицы
Решение задач Вид. 1. В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 3,6; 3,8; 4,3. Тогда несмещенная оценка дисперсии равна … · 0,13 · 0,065 · 3,9 · 0,7
Решение: Несмещенная оценка дисперсии вычисляется по формуле:
2. Проведено пять измерений (без систематических ошибок) некоторой случайной величины (в мм): 2,1; 2,3;; 2,7; 2,9. Если несмещенная оценка математического ожидания равна 2,48, то равно … · 2,4 · 2,5 · 2,6 · 2,48 Решение: Несмещенная оценка математического ожидания вычисляется по формуле: Следовательно, 3. Проведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 8, 9, · 2,5 · 2,0 · 0 · 1,5 Решение: Вычислим предварительно значение Для вычисления выборочной дисперсии применим формулу Тогда 4. Проведено пять измерений (без систематических ошибок) некоторой случайной величины (в мм): 4,5; 5,2; 6,1; 7,8, 8,3. Тогда несмещенная оценка математического ожидания равна … · 6,38 · 6,42 · 6,1 · 6,4 Решение: Несмещенная оценка математического ожидания вычисляется по формуле 5. В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 15; 18; 21; 24. Тогда выборочная дисперсия равна … · 11,25 · 19,5 · 15 · 21,25
Решение: Выборочная дисперсия вычисляется по формуле Вид. 1. Из генеральной совокупности извлечена выборка объема
Тогда выборочное среднее квадратическое отклонение равно …
· · · 10,46 ·
Решение: Выборочное среднее квадратическое отклонение вычисляется как , и 2. По выборке объема · 2,0 · 4,0 · 3,24 · 1,8 Решение: Исправленное среднее квадратическое отклонение вычисляется как
3. Из генеральной совокупности извлечена выборка объема
Тогда несмещенная оценка математического ожидания равна …
· 13,14 · 13,0 · 13,34 · 13,2 Решение: Несмещенная оценка математического ожидания вычисляется по формуле Вид 1. Если все варианты
Для исходного вариационного ряда выборочную дисперсию можем вычислить по формуле
|

 , 12. Если несмещенная оценка математического ожидания равна 10, то выборочная дисперсия будет равна …
, 12. Если несмещенная оценка математического ожидания равна 10, то выборочная дисперсия будет равна … :
: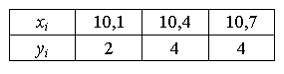
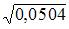
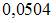

 найдена выборочная дисперсия
найдена выборочная дисперсия  . Тогда исправленное среднее квадратическое отклонение равно …
. Тогда исправленное среднее квадратическое отклонение равно … :
:
 исходного вариационного ряда увеличить в два раза, то выборочная дисперсия
исходного вариационного ряда увеличить в два раза, то выборочная дисперсия  …
… , где
, где  . Вычислив предварительно
. Вычислив предварительно 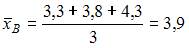 , получаем
, получаем  .
.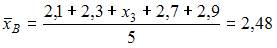 .
.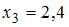 .
. . Так как несмещенная оценка математического ожидания вычисляется по формуле:
. Так как несмещенная оценка математического ожидания вычисляется по формуле:  . Следовательно,
. Следовательно,  .
. .
. .
. . То есть
. То есть  .
. , получаем
, получаем  .
.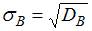 , где
, где  . Тогда
. Тогда 
 .
. , где
, где  . Тогда
. Тогда  .
. . То есть
. То есть  .
. .
.


