Выборочная средняя и выборочная дисперсия.
Точечные оценки. Выборочная средняя и выборочная дисперсия.
Оценки параметров генеральной совокупности, полученные на основании выборки, называются статистическими. Если статистическая оценка характеризуется одним числом, она называется точечной. К числу таких оценок относятся выборочная средняя и выборочная дисперсия.
Выборочная средняя определяется как среднее арифметическое полученных по выборке значений:
где
Выборочная дисперсия представляет собой среднюю арифметическую квадратов отклонений вариант от их выборочной средней:
Для расчетов может быть использована также формула
где
Статистическая оценка является случайной величиной и меняется в зависимости от выборки. Если математическое ожидание статистической оценки равно оцениваемому параметру генеральной совокупности, то такая оценка называется несмещенной, если не равно – то смещенной.
Выборочная средняя является оценкой математического ожидания случайной величины и представляет собой несмещенную оценку. Выборочная дисперсия оценивает дисперсию генеральной совокупности и является смещенной оценкой. Для устранения смещенности выборочной дисперсии ее умножают на величину
Величину
Модой
Медианой
Если дискретный вариационный ряд имеет
Если дискретный вариационный ряд в ранжированной совокупности имеет
Коэффициент вариации
В некоторых случаях для удобства расчетов при определении статистических оценок переходят к условным вариантам. Например, если варианты
где В этом случае
Для изменения значения варианты можно ввести также условные варианты путем использования масштабного множителя:
где
Пример 1. Из генеральной совокупности извлечена выборка объема
Найти смещенную оценку генеральной средней.
Решение. Несмещенной оценкой генеральной средней является выборочная средняя
Пример 2. Найти выборочную среднюю по данному распределению выборки:
Решение. так как выборочные значения – большие числа, то целесообразно ввести условные варианты. В качестве ложного нуля выбираем
Определяем выборочную среднюю После этого находим
Пример 3. Найти несмещенную оценку дисперсии случайной величины
Решение. Находим выборочную среднюю
Для вычисления выборочной дисперсии используем формулу
Находим несмещенную оценку дисперсии («исправленную» выборочную дисперсию):
|

 ,
, - варианта выборки;
- варианта выборки; - частота варианты;
- частота варианты; - объем выборки.
- объем выборки. .
. ,
, - выборочная средняя квадратов вариант выборки.
- выборочная средняя квадратов вариант выборки. и получают
и получают .
. называют несмещенной или «исправленной» выборочной дисперсией.
называют несмещенной или «исправленной» выборочной дисперсией. дискретного вариационного ряда называется вариант, имеющую наибольшую частоту.
дискретного вариационного ряда называется вариант, имеющую наибольшую частоту. дискретного вариационного ряда называется вариант, делящий ряд на две равные части.
дискретного вариационного ряда называется вариант, делящий ряд на две равные части. членов в ранжированной совокупности:
членов в ранжированной совокупности:  , то
, то .
. членов:
членов: 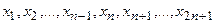 , то
, то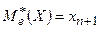 .
. -. Коэффициент вариации показывает сколько процентов от
-. Коэффициент вариации показывает сколько процентов от  составляет среднее квадратическое отклонение.
составляет среднее квадратическое отклонение. ,
, - произвольно выбранное число (ложный нуль), такое, при котором условные варианты принимают небольшие значения.
- произвольно выбранное число (ложный нуль), такое, при котором условные варианты принимают небольшие значения. ,
,  ,
, .
. ,
, (
( выбирается положительным или отрицательным целым числом).
выбирается положительным или отрицательным целым числом). :
: .
. и рассчитываем
и рассчитываем  по формуле
по формуле  :
: .
. .
. на основании данного распределения выборки:
на основании данного распределения выборки: .
. ,
, .
. .
.


