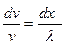Дальнее взаимодействие
Будем смотреть коллективное изменение скорости частиц. Определим количество частиц в объеме 2πρdρdx
dv – суммарное изменение скорости всех частиц, попавших в объём 2πρdρdx Смотрим изменение скорости в данном направлении δ v – на сколько уменьшится скорость δv =v(1-cosθ) dv=2πρdρdx∙n∙δv Если проинтегрировать по ρ от d ρ~ dv = Дебаевские радиус 1) Если размер плазмы меньше дебаевского радиуса, то это не плазма, а если больше то плазма 2)Дебаевский радиус – размер экранировки Когда сила взаимодействия между частицами уменьшается в е раз – радиус Дебая d – радиус Дебая Заменив ∞ на d мы получим придела от 0 до
После подстановки dv =
В огромном интервале плотностей и температур
Изменение траектории плавное Как определить длину свободного пробега для дальнодействующего взаимодействия?
То расстояние, которое они пробегают и отклоняются на
|



 до ∞ мы получим расходящийся интеграл. При данных ρ θ изменяется от
до ∞ мы получим расходящийся интеграл. При данных ρ θ изменяется от  до 0
до 0

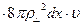
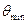 При θ→0
При θ→0  = 2
= 2 
 W =
W = 

 - кулоновский логарифм
- кулоновский логарифм  .
.