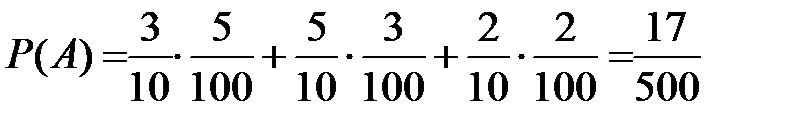Формула полной вероятности. Как говорилось ранее, эскон любого объекта задает его физическое состояние в любой момент времени, то есть является его управителем
Формула полной вероятности. Пусть имеется группа событий H 1, H 2,..., Hn, обладающая следующими свойствами: 1) все события попарно несовместны: Hi 2) их объединение образует пространство элементарных исходов W:
 . .
Пусть А – некоторое событие: А Ì W (диаграмма Венна представлена на рисунке 8). Тогда имеет место формула полной вероятности: P (A) = P (A / H 1) P (H 1) + P (A / H 2) P (H 2) +...+ P (A / Hn) P (Hn) = Доказательство. Очевидно: A = P (A) = P ( Если учесть, что по теореме умножения P ( Пример. В магазине продаются электролампы производства трех заводов, причем доля первого завода - 30%, второго - 50%, третьего - 20%. Брак в их продукции составляет соответственно 5%, 3% и 2%. Какова вероятность того, что случайно выбранная в магазине лампа оказалась бракованной. Пусть событие H 1 состоит в том, что выбранная лампа произведена на первом заводе, H 2 на втором, H 3 - на третьем заводе. Очевидно: P (H 1) = 3/10, P (H 2) = 5/10, P (H 3) = 2/10. Пусть событие А состоит в том, что выбранная лампа оказалась бракованной; A/Hi означает событие, состоящее в том, что выбрана бракованная лампа из ламп, произведенных на i -ом заводе. Из условия задачи следует: P (A/H 1) = 5/10; P (A/H 2) = 3/10; P (A/H 3) = 2/10 По формуле полной вероятности получаем
|

 Hj =Æ; i, j =1,2,..., n; i¹j;
Hj =Æ; i, j =1,2,..., n; i¹j;
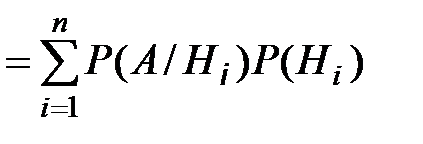
 , причем все события
, причем все события 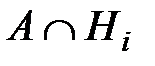 (i = 1,2,..., n) попарно несовместны. Отсюда по теореме сложения вероятностей получаем
(i = 1,2,..., n) попарно несовместны. Отсюда по теореме сложения вероятностей получаем ) + P (
) + P ( ) +...+ P (
) +...+ P (
 ) = P (A/H i) P (H i) (i = 1,2,..., n), то из последней формулы легко получить приведенную выше формулу полной вероятности.
) = P (A/H i) P (H i) (i = 1,2,..., n), то из последней формулы легко получить приведенную выше формулу полной вероятности.