РЕШЕНИЕ ДИОФАНТОВЫХ УРАВНЕНИЙ
РЕШЕНИЕ ДИОФАНТОВЫХ УРАВНЕНИЙ
Задача Диофанта: решить уравнение в целых числах: Решение существует только в том случае, если числа
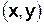 . Общее решение описывается формулой (1).
Для нахождения частного решения воспользуемся алгоритмом Евклида поиска наибольшего общего делителя НОД(a,b). Дополнительное условие: a > b>0. Обозначим Нулевой шаг алгоритма Евклида записывается в виде: или
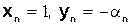 . Тогда оно примет следующий вид:
Теперь осуществим обратный ход. Из равенств (n-1) и (n) исключим где Равенство (n-1) приведено к следующему виду:
Аналогичным образом исключим
Таким образом, возникает цепочка равенств следующего вида:
Используя последние из чисел найденных последовательностей, приходим к тождеству:
Учитывая, что
|
.
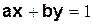взаимно просты. В таком случае решений бесконечно много. Если найдено решение 
.
.
,
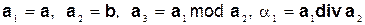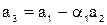. Аналогичным образом записываются и последующие шаги алгоритма Евклида вплоть до шага с номером n, когда остаток станет равным единице: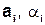
.
: 
,
.
.
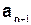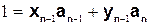, используя равенство (n-2):
, т.е.
, где 
.
.
.
.
, приходим к выводу, что решением уравнения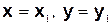 
.
