Моделирование временного ряда
В общем случае каждый уровень временного можно представить как функцию четырех компонент: f (t), S (t), U (t), f (t) – тренд (долговременная тенденция) развития; S (t) – сезонная компонента; U (t) –циклическая компонента;
В модели временного ряда принято выделять две основные составляющие: детерминированную (систематическую) и случайную. Под детерминированной составляющей временного ряда Детерминированная составляющая может содержать следующие структурные компоненты: 1) тренд, или тенденция f (t), представляет собой устойчивую закономерность, наблюдаемую в течение длительного периода времени. Обычно тренд (тенденция) описывается с помощью той или иной неслучайной функции f тр(t) (аргументом которой является время), как правило, монотонной. Эту функцию называют функцией тренда, или просто – трендом. 2) Сезонная компонента s(t) связана с наличием факторов, действующих с заранее известной периодичностью. Это регулярные колебания, которые носят периодический или близкий к нему характер и заканчиваются в течение года. Типичные примеры сезонного эффекта: изменение загруженности автотрассы по временам года, пик продаж товаров для школьников в конце августа – начале сентября. Спрос на пластические операции сезонный: в осенне-зимний период обращений больше. Типичным примером являются сильные колебания объема товарно-материальных запасов в сезонных отраслях Сезонная компонента со временем может меняться, либо иметь плавающий характер. 3) Циклическая компонента u (t) – неслучайная функция, описывающая длительные периоды (более одного года) относительного подъема и спада и состоящая из циклов переменной длительности и амплитуды. Примером циклической (конъюнктурной) компоненты являются волны Кондратьева, демографические «ямы» и т.п. Подобная компонента весьма характерна для рядов макроэкономических показателей. Здесь циклические изменения обусловлены взаимодействием спроса и предложения, а также наложением таких факторов, как истощение ресурсов, погодные условия, изменения в налоговой политике и т.п. Отметим, что циклическую компоненту крайне трудно идентифицировать формальными методами, исходя только из данных изучаемого ряда. 4) Случайная компонента В анализе случайного компонента экономических временных рядов важную роль играет сравнение случайной величины В зависимости от вида связи между этими компонентами может быть построена либо аддитивная модель: Y (t) =f (t)+ S (t)+ U (t)+ либо мультипликативная модель: Y (t) =f (t)× S (t)× U (t)+ В процессе формирования значений временных рядов не всегда участвуют все четыре компоненты. Однако во всех случаях предполагается наличие случайной составляющей. Тренды. Проводя разложение ряда на компоненты, мы, как правило, подразумеваем под трендом изменение среднего уровня переменной, то есть тренд среднего. В рамках анализа тренда среднего чаще всего используют полиномиальный тренд:
Для p = 1 имеем линейный тренд. AR(p) -авторегрессионая модель порядка p. Модель имеет вид:
где
Задача заключается в том, чтобы определить Термин авторегрессия для обозначения модели (3.4) используется потому, что она фактически представляет собой модель регрессии, в которой регрессорами служат лаги изучаемого ряда После построения любой модели временного ряда, прежде, чем прогнозировать по этой модели, нужно убедиться в ее адекватности, т.е. убедиться, что остатки Критерий Дарбина-Уотсона является наиболее распространенным критерием для проверки корреляции внутри ряда. Если величина
|

 (t), отражающих закономерность и случайность развития. Где
(t), отражающих закономерность и случайность развития. Где понимают числовую последовательность, элементы которой вычисляются по определенному правилу как функция времени t. Исключив детерминированную составляющую из данных, мы получим колеблющийся вокруг нуля ряд, который может в одном предельном случае представлять случайные скачки, а в другом – плавное колебательное движение.
понимают числовую последовательность, элементы которой вычисляются по определенному правилу как функция времени t. Исключив детерминированную составляющую из данных, мы получим колеблющийся вокруг нуля ряд, который может в одном предельном случае представлять случайные скачки, а в другом – плавное колебательное движение. с хорошо изученной формой случайных процессов - стационарными случайными процессами.
с хорошо изученной формой случайных процессов - стационарными случайными процессами. (3.3)
(3.3)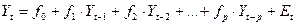 (3.4)
(3.4) - зависимая переменная в момент времени t.
- зависимая переменная в момент времени t. - оцениваемые параметры.
- оцениваемые параметры. 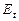 - ошибка от влияния переменных, которые не учитываются в данной модели.
- ошибка от влияния переменных, которые не учитываются в данной модели.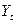 . По определению авторегрессии ошибки Et являются белым шумом и некоррелированы с лагами
. По определению авторегрессии ошибки Et являются белым шумом и некоррелированы с лагами  некоррелированы между собой.
некоррелированы между собой. , где
, где  - расхождение между фактическими и расчетными уровнями, имеет значение, близкое к 2, то можно считать модель достаточно адекватной. Когда адекватная модель найдена, можно делать прогнозы на один или несколько периодов вперед.
- расхождение между фактическими и расчетными уровнями, имеет значение, близкое к 2, то можно считать модель достаточно адекватной. Когда адекватная модель найдена, можно делать прогнозы на один или несколько периодов вперед.


