Основные описательные статистики для временных рядов.Среднее и дисперсия временного ряда рассчитываются по формулам:
Выборочная автоковариация k -го порядка вычисляется как
Статистической оценкой автокорреляции k -го порядка для стационарных процессов является выборочный коэффициент автокорреляции: Стационарным процессом называется такой случайный процесс, вероятностные свойства которого с течением времени не изменяются. Он протекает в приблизительно однородных условиях и имеет вид непрерывных случайных колебаний вокруг некоторого среднего значения. Причем ни средняя амплитуда, ни его частота не обнаруживают с течением времени существенных изменений. 3.3.1 "Наивные" модели прогнозирования При создании "наивных" моделей предполагается, что некоторый последний период прогнозируемого временного ряда лучше всего описывает будущее этого прогнозируемого ряда, поэтому в этих моделях прогноз, как правило, является очень простой функцией от значений прогнозируемой переменной в недалеком прошлом. Самой простой моделью является Y(t+1)=Y(t), что соответствует предположению, что "завтра будет как сегодня". Вне всякого сомнения, от такой примитивной модели не стоит ждать большой точности. Она не только не учитывает механизмы, определяющие прогнозируемые данные (этот серьезный недостаток вообще свойственен многим статистическим методам прогнозирования), но и не защищена от случайных флуктуаций, она не учитывает сезонные колебания и тренды. Впрочем, можно строить "наивные" модели несколько по-другому Y(t+1)=Y(t)+[Y(t)-Y(t-1)], Y(t+1)=Y(t)*[Y(t)/Y(t-1)], такими способами мы пытаемся приспособить модель к возможным трендам. Y(t+1)=Y(t-s), это попытка учесть сезонные колебания
|
.
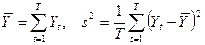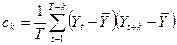
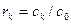. При анализе изменения величин c k и rk в зависимости от значения k обычно пользуются выборочными автоковариационной и автокорреляционной функциями, определяемыми как последовательност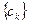и 
и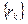 
, соответственно. Выборочная автокорреляционная функция играет особую роль в анализе стационарных временных рядов, поскольку может быть использована в качестве инструмента для распознавания типа процесса. При этом обычно анализируют график автокорреляционной функции, называемый коррелограммой.
