Методы решения задач классификации
5.1 Опис процесу класифікації Мета процесу класифікації полягає в побудові такої моделі, яка використовує незалежні прогнозуючі атрибути як вхідні параметри й видає значення залежного атрибута. Процес класифікації полягає в розбивці множини об'єктів на класи за певним критерієм. Для проведення класифікації за допомогою математичних методів необхідно мати формальний опис об'єкта, яким можна оперувати, використовуючи математичний апарат класифікації. Таким описом найчастіше виступає база даних. Кожний запис бази даних несе інформацію про деяку властивість об'єкта. Набір вихідних даних (вибірку даних) розбивають на дві множини: навчальна (training set) і тестова (test set). У навчальну вибірку входять об'єкти, для яких відомі значення як незалежних, так і залежних змінних. На підставі навчальної вибірки будується модель визначення значення залежної змінної. Її часто називають функцією класифікації. Для одержання максимально точної функції до навчальної вибірки пред'являються такі основні вимоги: - кількість об'єктів, що входять у вибірку, повинна бути досить великою. Чим більше об'єктів, тим побудована на їх основі функція класифікації буде точніше; - у вибірку повинні входити об'єкти, що представляють всі можливі класи; - для кожного класу вибірка повинна мати достатню кількість об'єктів. Тестова (test set) множина також містить вхідні й вихідні значення прикладів. Тут вихідні значення використовуються для перевірки працездатності моделі. Процес класифікації складається із двох етапів: конструювання моделі і її використання. a) Конструювання моделі: опис множини визначених класів. 1) Кожний приклад набору даних ставиться до одного з визначених класів. 2) На цьому етапі використовується навчальна множина, на ньому відбувається конструювання моделі. 3) Отримана модель представлена класифікаційними правилами, деревом рішень або математичною формулою. б) Використання моделі: класифікація нових або невідомих значень. 1) Оцінка правильності (точності) моделі. Відомі значення з тестового набору порівнюються з результатами використання отриманої моделі. За рівень точності приймається відсоток правильно класифікованих прикладів у тестовій множині. 2) Якщо точність моделі припустима, можливе використання моделі для класифікації нових прикладів, клас яких невідомий. Основні проблеми, з якими зіштовхуються при вирішенні задач класифікації, - це незадовільна якість вхідних даних, у яких зустрічаються як помилкові дані, так і пропущені значення, різні типи атрибутів - числові й категоріальні, різна значимість атрибутів, а також так звані проблеми overfitting і underfltting. Суть першої з них полягає в тім, що класифікаційна функція при побудові "занадто добре" адаптується до даних, і помилки, що зустрічаються в них, і аномальні значення намагається інтерпретувати як частину внутрішньої структури даних. Очевидно, що така модель буде некоректно працювати надалі з іншими даними, де характер помилок буде трохи іншим. Терміном underfltting позначають ситуацію, коли спостерігається занадто велика кількість помилок при перевірці класифікатора на навчальній множині. Це означає, що особливих закономірностей у даних не було виявлено і або їх немає взагалі, або необхідно вибрати інший метод їхнього виявлення. Геометрична інтерпретація задачі класифікації Задача класифікації має геометричну інтерпретацію. Розглянемо її на прикладі із двома незалежними змінними, що дозволить представити її у двовимірному просторі (рис. 3.1). Кожному об'єкту ставиться у відповідність точка на площині. Символи "+" і "-" позначають приналежність об'єкта до одного з двох класів. Очевидно, що дані мають чітко виражену структуру: всі точки класу "+" зосереджені в центральній області. Побудова класифікаційної функції зводиться до побудови поверхні, що обводить центральну область. Вона визначається як функція, що має значення "+" усередині обведеної області й "-" — поза нею.
Рисунок 5.1 - Класифікація у двовимірному просторі Як видно з рис. 5.1, є кілька можливостей для побудови такої області. Вид функції залежить від застосовуваного алгоритму. Для класифікації використовуються різні методи. Основні з них: · класифікація за допомогою штучних нейронних мереж; · статистичні методи, зокрема, логістична регресія; · класифікація за допомогою методу найближчого сусіда; · класифікація методом опорних векторів; · класифікація за допомогою дерев рішень; · класифікація дискримінантним аналізом. 5.2 Оцінка якості моделі класифікації Оцінка точності класифікації може проводитися за допомогою крос-перевірки. Крос-перевірка (сross-validation) - це процедура оцінки точності класифікації на даних з тестової множини, що також називають крос-перевірочною множиною. Точність класифікації тестової множини порівнюється з точністю класифікації навчальної множини. Якщо класифікація тестової множини дає приблизно такі ж результати по точності, як і класифікація навчальної множини, вважається, що дана модель пройшла крос-перевірку. Для візуалізації результатів крос-перевірки найчастіше використовують таблицю спряженості. Розглянемо докладніше процес її створення. Для вирішення задачі класифікації використовується таблиця, у якій уже є вихідний стовпець, що містить клас об'єкта. Після застосування навчального алгоритму додається ще один стовпець із вихідним полем, але його значення вже обчислюються, використовуючи побудовану модель. При цьому значення в стовпцях можуть відрізнятися. Чим більше таких відмінностей, тим гірше побудована модель класифікації.
Рисунок 5.2 - Таблиця спряженості Нижче представлено пояснення щодо складових таблиці. TP (True Positives) - кількість вірно класифікованих позитивних прикладів (так звані істинно позитивні випадки); TN (True Negatives) - кількість вірно класифікованих негативних прикладів (істинно негативні випадки); FN (False Negatives) - кількість позитивних прикладів, класифікованих як негативні (помилка I роду). Це так званий «помилковий пропуск», що коли цікавить нас подія помилково не виявляється (хибно негативні приклади); FP (False Positives) - негативні приклади, класифіковані як позитивні (помилка II роду); Це «помилкове виявлення», тому що при відсутності події помилково виноситься рішення про її присутність (хибно позитивні випадки). Що є позитивною подією, а що - негативною, залежить від конкретної задачі. На головній діагоналі показана кількість правильно класифікованих прикладів, на побічній діагоналі – кількість неправильно класифікованих прикладів. Якщо кількість неправильно класифікованих прикладів досить велика, це говорить про погано побудовану модель, потрібно змінити параметри побудови моделі, збільшити навчальну вибірку або змінити набір вхідних полів. Якщо ж кількість неправильно класифікованих прикладів незначна, це може говорити про те, що дані приклади є аномаліями. У цьому випадку можна подивитися, чим же характеризуються такі приклади й, можливо, додати новий клас для їхньої класифікації. Ще один засіб, який застосовується для подання та оцінки результатів бінарної класифікації в машинному навчанні - ROC-аналіз. ROC-аналіз дозволяє провести оцінку якості моделі класифікатора, порівняти прогностичну силу декількох моделей, визначити оптимальну точку відсікання для віднесення об'єктів до того чи іншого класу. При цьому передбачається, що у класифікатора є додаткові параметри, що дозволяють вже після проведеного навчання варіювати співвідношення помилок першого й другого роду. В основі ROC-аналізу лежить побудова графіків - ROC-кривих (Receiver Operator Characteristic). Назва прийшла із систем обробки сигналів. Оскільки класів два, один з них називається класом з позитивними наслідками, другий - з негативними. ROC-крива показує залежність кількості вірно класифікованих позитивних прикладів від кількості невірно класифікованих негативних прикладів. У термінології ROC-аналізу перші називаються істинно позитивною, другі - хибно негативною множиною. Як уже говорилося вище, у класифікатора є деякий параметр, варіюючи який, ми будемо одержувати ту або іншу розбивку на два класи. Цей параметр часто називають порогом, або точкою відсікання (cutoff value). При аналізі використовуються значення з таблиці спряженості, але найчастіше оперують не абсолютними показниками, а відносними – частками (rates) вираженими у відсотках: Так, частка істинно позитивних прикладів (True Positives Rate):
Частка хибно позитивних прикладів (False Positives Rate):
Введемо ще два визначення: чутливість і специфічність моделі. Ними визначається об'єктивна цінність будь-якого бінарного класифікатора. Чутливість (Sensitivity) - це і є частка істинно позитивних випадків:
Специфічність (Specificity) - частка істинно негативних випадків, які були правильно ідентифіковані моделлю:
Зауважимо, що Модель із високою чутливістю часто дає істинний результат при наявності позитивного результату (виявляє позитивні приклади). Навпаки, модель із високою специфічністю частіше дає істинний результат при наявності негативного результату (виявляє негативні приклади). ROC-крива будується у такий спосіб: для кожного значення порога відсікання, що змінюється від 0 до 1 із кроком dx (наприклад, 0.01) розраховуються значення чутливості Se і специфічності Sp. Як альтернатива порогом може бути кожне наступне значення приклада у вибірці. Будується графік залежності: по осі Y відкладається чутливість Se, по осі X - 100%-Sp (сто відсотків мінус специфічність). Для ідеального класифікатора графік ROC-кривої проходить через верхній лівий кут, де частка істинно позитивних випадків становить 100% або 1.0 (ідеальна чутливість), а частка хибно позитивних прикладів дорівнює нулю. Тому чим ближче крива до верхнього лівого кута, тим вища прогностична здатність моделі. Навпаки, чим менше вигин кривої й чим ближче вона розташована до діагональної прямої, тим менш ефективна модель. Діагональна лінія відповідає "марному" класифікатору, тобто повної нерозрізненості двох класів.
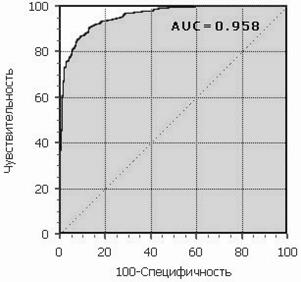
Рисунок 5.3 - ROC-крива Графік часто доповнюють прямою y=x. При візуальній оцінці ROC-кривих розташування їх відносно один одного вказує на їхню порівняльну ефективність. Крива, розташована вище й лівіше, свідчить про більшу прогностичну здатність моделі. Так, на рисунку 3.4 дві ROC-криві сполучені на одному графіку. Видно, що модель "A" краща. Візуальне порівняння кривих ROC не завжди дозволяє виявити найбільш ефективну модель. Своєрідним методом порівняння ROC-кривих є оцінка площі під кривими. Теоретично вона змінюється від 0 до 1.0, але, через те, що модель завжди характеризується кривою, розташованою вище позитивної діагоналі, то звичайно говорять про зміни від 0.5 ("марний" класифікатор) до 1.0 ("ідеальна" модель). Ця оцінка може бути отримана безпосередньо обчисленням площі під багатогранником, обмеженим праворуч і знизу осями координат і ліворуч угорі - експериментально отриманими точками (рис. 5.5). Чисельний показник площі під кривою називається AUC (Area Under Curve). З великими допущеннями можна вважати, що чим більше показник AUC, тим кращою прогностичною силою володіє модель.
Рисунок 5.4 - Порівняння ROC-кривих Однак варто знати, що: - показник AUC призначений скоріше для порівняльного аналізу декількох моделей; - AUC не містить ніякої інформації про чутливість і специфічність моделі. У літературі іноді приводиться така експертна шкала для значень AUC, по якій можна судити про якість моделі: Таблиця 5.1 - Оцінка якості класифікації на підставі AUC
Ідеальна модель володіє 100% чутливістю й специфічністю. Однак на практиці домогтися цього неможливо, більше того, неможливо одночасно підвищити й чутливість, і специфічність моделі.
Рисунок 5.5 - Площа під ROC-кривою Компроміс знаходиться за допомогою порога відсікання, тому що його граничне значення впливає на співвідношення Se і Sp. Можна говорити про задачу знаходження оптимального порога відсікання (optimal cutoff value). Поріг відсікання потрібний для того, щоб застосовувати модель на практиці: відносити нові приклади до одного із двох класів. Для визначення оптимального порога потрібно задати критерій його визначення, тому що в різних задачах присутня своя оптимальна стратегія. Критеріями вибору порога відсікання можуть виступати: - Вимога максимальної сумарної чутливості й специфічності моделі, тобто: - Вимога балансу між чутливістю й специфічністю, тобто коли У другому випадку порогом є точка перетинання двох кривих, коли по осі X відкладається поріг відсікання, а по осі Y - чутливість і специфічність моделі (рис. 5.6).
5.3 Скоринговые модели для оценки кредитоспособности заемщиков – пример задачи классификации на основе логистической регрессии Технологии кредитного скоринга – автоматической оценки кредитоспособности физического лица – в банковской сфере традиционно уделяется повышенное внимание. Сегодня можно сказать, что экспертные методы уходят в прошлое, и все чаще при разработке скоринговых моделей обращаются к алгоритмам Data Mining. Классическую скоринговую карту можно построить при помощи логистической регрессии на основе накопленной кредитной истории, применив к ней ROC-анализ для управления рисками. Кроме того, хорошие и легко интерпретируемые модели можно получить, используя деревья решений.
|



 . (5.1)
. (5.1) . (5.2)
. (5.2) . (5.3)
. (5.3)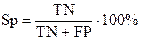 . (5.4)
. (5.4) . (5.5)
. (5.5)



 :
: 




