Скоринговая карта на основе логистической регрессии
Базовым статистическим алгоритмом, который строит аналог скоринговой карты, является логистическая регрессия. На практике логистическая регрессия используется для решения задач классификации с линейно-разделяемыми двумя классами. Задано множество записей, содержащих значения признаков В модели логистической регрессии свободные переменные
Требуется найти такое значение вектора параметров
где Введем в рассмотрение понятие «шанс», который определяется как вероятность того, что событие произошло (шанс успеха), разделенная на вероятность того, что событие не произошло (шанс неуспеха). Шансы и вероятности содержат одну и ту же информацию, но по-разному ее выражают. Если вероятность того, что событие произойдет, обозначить Определим также так называемое отношение шансов, или отношение несогласия (odds ratio – OR), являющееся отношением шансов того, что событие произойдет, к шансам того, что событие не произойдет. Очевидно, что если OR=1, то модель оказывается бесполезной, и чем сильнее отношение шансов отличается от 1, тем более значимой будет модель.
|

 и значения зависимой переменной
и значения зависимой переменной  , которая указывает, к какому классу относится запись.
, которая указывает, к какому классу относится запись. связаны зависимостью
связаны зависимостью , где
, где 
 , которое бы доставляло минимум сумме S:
, которое бы доставляло минимум сумме S:
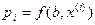 вычисляется по модели для записи с номером і. Значения
вычисляется по модели для записи с номером і. Значения  находится в интервале от 0 до 1 и указывает вероятность принадлежности записи к одному из двух классов.
находится в интервале от 0 до 1 и указывает вероятность принадлежности записи к одному из двух классов. , то шансы этого события будут равны
, то шансы этого события будут равны  . Например, если вероятность выздоровления составляет 0,3, то шансы выздороветь равны 0,3/(1-0,3)=0,43.
. Например, если вероятность выздоровления составляет 0,3, то шансы выздороветь равны 0,3/(1-0,3)=0,43.


