Скоринговая модель на основе дерева решений
Теперь воспользуемся другим инструментом — деревом решений. Используйте таблицу, в которой вы уже создали выходное поле Класс заемщика. Добавьте в сценарий одноименный узел через Мастер обработки.
На следующем шаге в качестве желаемого способа построения дерева оставьте режим автоматического построения. Запустив его нажатием кнопки Пуск, пройдите по шагам мастера дальше и выберите нужные визуализаторы, отметьте флажками Дерево решений, Значимость атрибутов, Что-если, Таблица сопряженности. В результате работы алгоритма было выявлено 18 правил. Точность классификации на обучающем множестве составила 85 %, на тестовом — 87 %. Визуализатор Дерево решений позволяет увидеть полученный набор правил в схематическом виде, а также выводит показатели достоверности и поддержки для каждого узла (рис. 4.19). Это и есть скоринговая модель. Она менее привычна, поскольку здесь не начисляются баллы за характеристики заемщика, но тоже объясняет результат классификации того или иного заемщика. В принципе, достоверность каждого правила можно воспринимать как итоговый скоринговый балл с той оговоркой, что для плохих заемщиков он равен величине, полученной вычитанием из 100%-ного значения достоверности.
Рисунок 5.19 – Скоринговая модель – дерево решений Теперь откройте таблицы сопряженности этого дерева решений.
Рисунок 5.20 – Таблицы сопряженности для рабочей и тестовой выборки Оказывается, в сравнении с моделью на основе логистической регрессии здесь совершенно другая ситуация. Дерево решений значительно чаще одобряет неблагонадежных заемщиков, потому что его построение идет в условиях несбалансированности классов. В результате доля дефолтных кредитов на тестовом множестве равна BR = 51 / 475 • 100 % = 10,7 %, что в 3 раза выше этого же показателя в логрегресионной модели (правда, уровень одобрений вырастает до 87,6%). Что делать, если такая ситуация не устраивает? В логистической регрессии для решения этой проблемы мы варьировали порогом отсечения, а в дереве решений такой возможности нет. Нам помогут специальные стратегии сэмплинга для уравновешивания обучающего множества: выборка с дублированием миноритарного класса (oversampling) и выборка с удалением примеров мажоритарного класса (undersampling). Поскольку примеров не так много (400 — с плохими клиентами и 1767 — с хорошими) и информация о каждом заемщике представляет ценность, имеет смысл использовать первый вариант — с дублированием. Пусть отношение издержек ошибочной классификации останется прежним: 1:4. Тогда, согласно правилу, к обучающей выборке нужно добавить 3 • 400 = 1200 примеров, и общее число записей составит 3367, а доля плохих увеличится до 47 %. Процедуру дублирования записей, принадлежащих к миноритарному классу, нужно осуществлять только на обучающем множестве. Для этой операции снова привлечем несколько узлов из группы Трансформация данных. Фильтр и Слияние данных (рис. 5.21). Построив дерево решений по сбалансированной выборке, убедитесь, что ситуация улучшилась: теперь на тестовом множестве модель чаще отказывает в выдаче хорошим заемщикам, нежели одобряет плохих. Эти результаты сравнимы с теми, которые выдает модель логистической регрессии. Таким образом, мы получили несколько скоринговых моделей. Варьируя порогами отсечения и применяя специальные приемы борьбы с несбалансированностью классов, можно подобрать ту модель, которая отвечает заданным потребностям кредитного учреждения по уровню одобрений заявок и ожидаемой доле просроченной задолженности. Проверять новых клиентов можно при помощи обработчика Скрипт.
Рисунок 5.21 – Сценарий для построения скоринговой модели на основе дерева решений 5.3.4 Интерактивное дерево решений До этого мы получали дерево, которое строилось автоматическим способом, то есть алгоритм на каждом шаге выбирал атрибут для разбиения по заданному критерию. Известно, что алгоритмы построения деревьев «жадные», поэтому не факт, что итоговое дерево будет наилучшим. В то же время иногда имеются экспертные знания, которые позволяют «вмешаться» в процесс формирования дерева и выбора атрибутов, а также порогов для разбиения. Возможно, это и не повысит точность модели, но правила станут более логичными, с точки зрения экспертов. Кредитный скоринг представляет собой тот самый случай, когда банковские аналитики имеют определенные знания и хотят, чтобы в модели ветвление по атрибутам осуществлялось в определенном порядке. Например, если имеются атрибуты Наличие квартиры и Стоимость квартиры, то разумно сразу после первого рассмотреть второй. Еще пример: после суммы кредита сразу желательно проанализировать первоначальный взнос. В аналитической платформе Deductor имеется возможность построения интерактивных деревьев решений. Зададимся целью построить скоринговую модель на прежней выборке, приняв во внимание следующие пожелания экспертов. 1. Первым атрибутом, по которому анализируют заемщика, должен быть атрибут Кредитная история. 2. Далее необходимо рассмотреть коэффициент О/Д. Всех клиентов нужно разбить на три категории: заемщики с низким О/Д (до 20 %), с умеренным (от 20 до 40 %) и высоким (от 40 %). Добавьте в сценарий новый узел дерева решений и на пятом шаге мастера поставьте переключатель в позицию Интерактивный режим. В результате открывшийся визуализатор Дерево решений не будет содержать ни одного узла. На панели инструментов нажмите кнопку Разбить текущий узел на подузлы..., откроется соответствующее окно (рис. 54.22).
Рисунок 5.22 – Окно выбора атрибута для разбиения в интерактивном режиме: первый шаг Слева в списке выводятся все атрибуты вместе с рассчитанными значениями прироста информации Gain Ratio, а справа — диаграммы распределения классов по подузлам. По умолчанию предлагается атрибут с максимальным значением Gain Ratio, но его можно переопределить. В данном случае ничего делать не нужно, поскольку разбиение и так начнется по атрибуту Кредитная история. Нажатие кнопки Ок приведет к тому, что в дерево добавится три узла этого атрибута со значениями нет данных, отрицательная, положительная. Продолжим разбиение дальше, выбрав узел Кредитная история = нет данных (рис. 5.23).
Рисунок 5.23 - – Окно выбора атрибута для разбиения в интерактивном режиме: второй шаг Здесь в качестве оптимального с точки зрения прироста информации предлагается атрибут Проживание. Переопределите его на ОД, %, указав в нижней части окна порог, равный 20. Затем для узла ОД, % >20 снова выберите разбиение по ОД, %, но уже с порогом 40, после чего нажмите кнопку Построить дерево, начиная с текущего узла. В результате ветвь дерева будет полностью готова (рис. 5.24). Аналогичным образом достраивается дерево для оставшихся узлов. Качество классификации, как и прежде, можно оценивать через таблицы сопряженности.
|

 Следующие два шага мастера аналогичны описанным ранее для узла Логистическая регрессия. Отметьте поля Код и Дата как информационные, а поля Просрочки и Тестовое множество – неиспользуемые. На четвертом шаге откроется окно выбора параметров алгоритма. Здесь не меняйте настройки, принятые по умолчанию, за исключением минимального количества примеров в узле, при котором будет создаваться новый. Задайте этот параметр равным примерно 1 % от объема обучающего множества (т.е. 20); меньшее значение может привести к появлению недостоверных правил, большее — к почти полному отсутствию таковых.
Следующие два шага мастера аналогичны описанным ранее для узла Логистическая регрессия. Отметьте поля Код и Дата как информационные, а поля Просрочки и Тестовое множество – неиспользуемые. На четвертом шаге откроется окно выбора параметров алгоритма. Здесь не меняйте настройки, принятые по умолчанию, за исключением минимального количества примеров в узле, при котором будет создаваться новый. Задайте этот параметр равным примерно 1 % от объема обучающего множества (т.е. 20); меньшее значение может привести к появлению недостоверных правил, большее — к почти полному отсутствию таковых.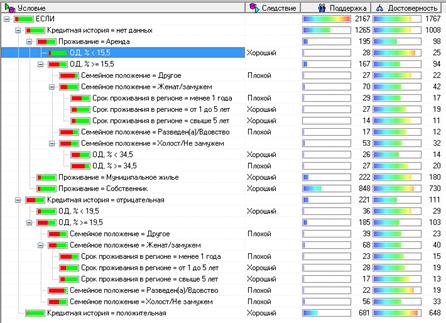
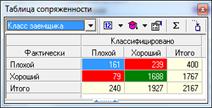




 Рисунок 5.24 – Дерево решений, построенное в интерактивном режиме
Рисунок 5.24 – Дерево решений, построенное в интерактивном режиме


