Критерий расщепления
Процесс создания дерева происходит сверху вниз, т.е. является нисходящим. В ходе процесса алгоритм должен найти такой критерий расщепления, иногда также называемый критерием разбиения, чтобы разбить множество на подмножества, которые бы ассоциировались с данным узлом проверки. Каждый узел проверки должен быть помечен определенным атрибутом. Существует правило выбора атрибута: он должен разбивать исходное множество данных таким образом, чтобы объекты подмножеств, получаемых в результате этого разбиения, являлись представителями одного класса или же были максимально приближены к такому разбиению. Последняя фраза означает, что количество объектов из других классов, так называемых "примесей", в каждом классе должно стремиться к минимуму. Существуют различные критерии расщепления. Наиболее известные - мера энтропии и индекс Gini. При помощи индекса Gini атрибут выбирается на основании расстояний между распределениями классов. Если дано множество T, включающее примеры из k классов, индекс Gini, т.е. gini(T), определяется по формуле:
где T - текущий узел, pj – вероятность (доля) класса j в узле T, n – количествообъектов, k – количество классов. Энтропия или прирост информации. Мера количества информации – это энтропия, а в нашем случае это мера разнообразия классов в узле. В результате разбиения должны образовываться узлы с меньшим разнообразием состояний выходной переменной. Следовательно, энтропия падает, а количество внутренней информации в узле растет. Формально энтропия определенного узла Т дерева решений определяется так:
Энтропия всего разбиения – сумма энтропий всех узлов, умноженных на долю записей каждого узла в общем числе записей: Энтропия всего разбиения – сумма энтропий всех узлов, умноженная на долю записей каждого узла в общем числе записей:
Для выбора атрибута расщепления используется критерий, называемый приростом информации или уменьшением энтропии:
В качестве наилучшего атрибута для использования в разбиении S выбирается тот, который обеспечивает наибольший прирост информации Gain(S). Большое дерево не означает, что оно "подходящее". Чем больше частных случаев описано в дереве решений, тем меньшее количество объектов попадает в каждый частный случай. Такие деревья называют "ветвистыми" или "кустистыми", они состоят из неоправданно большого числа узлов и ветвей, исходное множество разбивается на большое число подмножеств, состоящих из очень малого числа объектов. В результате "переполнения" таких деревьев их способность к обобщению уменьшается, и построенные модели не могут давать верные ответы. В процессе построения дерева, чтобы его размеры не стали чрезмерно большими, используют специальные процедуры, которые позволяют создавать оптимальные деревья, так называемые деревья "подходящих размеров" (Breiman,1984). Какой размер дерева может считаться оптимальным? Дерево должно быть достаточно сложным, чтобы учитывать информацию из исследуемого набора данных, но одновременно оно должно быть достаточно простым. Другими словами, дерево должно использовать информацию, улучшающую качество модели, и игнорировать ту информацию, которая ее не улучшает. Тут существует две возможные стратегии. Первая состоит в наращивании дерева до определенного размера в соответствии с параметрами, заданными пользователем. Определение этих параметров может основываться на опыте и интуиции аналитика, а также на некоторых "диагностических сообщениях" системы, конструирующей дерево решений. Вторая стратегия состоит в использовании набора процедур, определяющих "подходящий размер" дерева, они разработаны Бриманом, Куилендом и др. в 1984 году. Однако, как отмечают авторы, нельзя сказать, что эти процедуры доступны начинающему пользователю. Процедуры, которые используют для предотвращения создания чрезмерно больших деревьев, включают: сокращение дерева путем отсечения ветвей; использование правил остановки обучения. Следует отметить, что не все алгоритмы при конструировании дерева работают по одной схеме. Некоторые алгоритмы включают два отдельных последовательных этапа: построение дерева и его сокращение; другие чередуют эти этапы в процессе своей работы для предотвращения наращивания внутренних узлов.
|

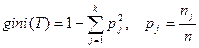
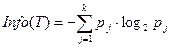
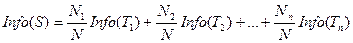 .
.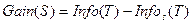 .
.


