Студопедия Главная Случайная страница Обратная связь

Разделы: Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Вычислить выражение


⇐ Предыдущая12



Вариант Выражение  
1.  
2.  
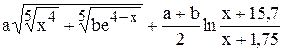
3.  
4.  
5.  
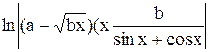
6.  
7.  
8.  
9.  
10.  
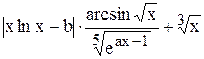
11.  
12.  
13.  
14.  
15.  
16.  
17.  
18.  
19.  
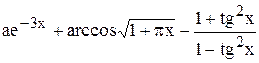
20.  
21.  
22.  
23.  
24.  
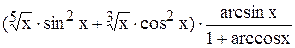
25.  

 

Решить уравнения

Вариант Уравнение Ответ
1. x = - 1.
2. x1 = 34; x2 = 2.
3. x = 4.
4. x1 = 0; x2 = 5.
5. x = 1.
6. x = 6.
7. x1 = 3; x2 = 4; .
8.
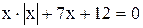
9. x1 = - 6; .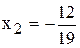
10. x1 = 0; x2 = - 6.
11. x1 = ± 6; x2 = ± 1.
12. x1 = - 7; x2 = 7.
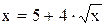
13. x =25
14. x =4
15. x1 = 25; x2 = 49.
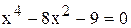
16. x1 = - 3; x2 = 3.
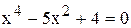
17. x1 = ± 2; x2 = ± 1.
18.
19. x1 = 0; x2 = 1.
20. x1 = - 2;
21. ;
22.
23.
24.  
25.  

 

 

Решить системы уравнений

Вариант Система уравнений Ответ
1. 1) x1 = 4, y1 = 2; 2) x2 = 2, y2 = 4;
2. 1) x = 5, y = 1; 2) x = 1, y = 5; 3) x = 2, y = 3; 4) x = 3, y = 2;
3. 1) x = 4, ; 2) x = 4, ; 3) x = 3, y = 2; 4) x = 3, y = - 2;
4. 1) x = 5, y = 2; 2) x = - 5, y = 2; 3) , y = - 25; 4) , y = - 25;
5. 1) x = 5, y = 4; 2) x = - 5, y = - 4; 3) x = 4i, y = - 5i; 4) x = - 4i, y = 5i;
6. 1) x = 3, y = 2; 2) x = - 3, y = - 2; 3) , ; 4) , ;
7. 1) x = 0, y = 0; 2) x = 4, y = 2; 3) x = - 2, y = - 4;
8. 1) x = 3, y = 1; 2) x = 1, y = 3;
9. 1) x = 3, y = 2; 2) x = - 2, y = - 3;
10. 1) x = 4, y = 3; 2) x = - 4, y = - 3; 3) x = 3i, y = - 4i; 4) x = - 3i, y = 4i;
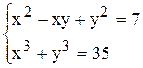
11. 1) x = 3, y = 2; 2) x = 2, y = 3;
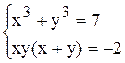
12. 1) x = 2, y = - 1; 2) x = - 1, y = 2
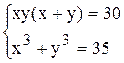
13. 1) x = 3, y = 2; 2) x = 2, y = 3;
14. 1) x = 3, y = 2; 2) x = - 3, y = - 2; 1) x = 3i, y = - 2i; 2) x = - 3i, y = 2i;
15. 1) x = 9, y = 1; 2) x = 1, y = 9;  
16. 1) x = 6, y = 12; 2) x = - 4,5, y = - 9;
17. 1) x = 2, y = 8; 2) x = 8, y = 2;
18. 1) x = 3, ; 2) , y = 3;
19. 1) x = 9, y = 7; 2) x = - 9, y = - 7;
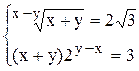
20. 1) x = 7, y = 5;
21. 1) x = 1, y = -1;
22.  
23. 1) x = 8, y = 4; 2) x = - 8, y = - 4;
24. 1) x = -1, y = -1; 2) x = 2, y = -1; 3) x = -1, y = 2;  
25. 1) x = 2, y = 1; 2) x = -2, y = -1; 3) x = , y = ; 4) x = , y = ;

Решить неравенства

Вариант Неравенства Ответ
1. , удовлетворяющие условию
2.
3.
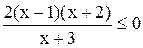
4.
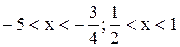
5.
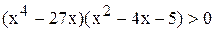
6.
7.
8.
9.
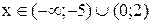
10.
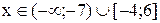
11.
12.
13.
14.
15.
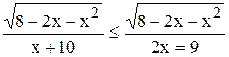
16.
17.
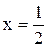
18.
19.
20.
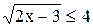
21.  
22.
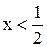
23.
24.
25.

 

Построить графики функций

Вариант Функция  
1.  
2.  
3.  
4.  
5.  
6.  
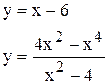
7.  
8.  
9.  
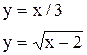
10.  
11.  
12.  
13.  
14.  
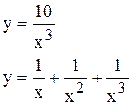
15.  
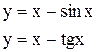
16.  
17.  
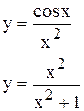
18.  
19.  
20.  
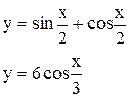
21.  
22.  
23.  
24.  
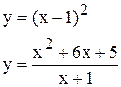
25.  

 

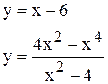
Вычисление определенного интеграла

Вариант Выражение Ответ
1.
2.
3.
4.
5.
6.
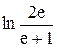
7.
8.
9.
10.
11.
12.
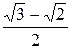
13.
14.  
15.
16.
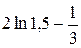
17.
18.
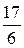
19.
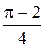
20.
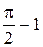
21.
22.
23.
24.
25.

 

Вычисление неопределенного интеграла

Вариант Интеграл Ответ
1.  
2.  
3.  
4.  
5.  
6.  
7.  
8.  
9.  
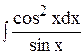
10.  
11.  
12.  
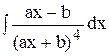
13.  
14.  
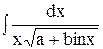
15.  
16.  
17.  
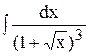
18.  
19.  
20.  
21.  
22.  
23.  
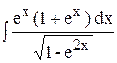
24.  
25.  

 

Найти производные от функций

Вариант Функция Ответ
1.
2.
3.
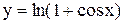
4.
5.
6.
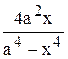
7.
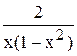
8.
9.
10.
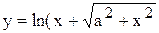
11.
12.
13.
14.
15.
16.
17.
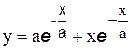
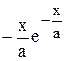
18.
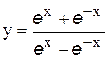
19.
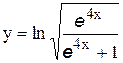
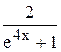
20.
21.
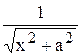
22.
23.
24.
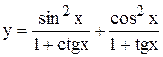
25.

 

Решить дифференциальные уравнения

Вариант Уравнение Ответ
1.
2.
3.
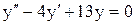
4.
5.
.
7.
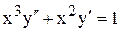
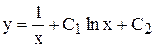
8.
9.
10.
11.
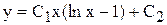
12.
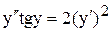
13.
14.
15.  
16.
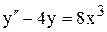
17.
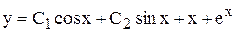
18.
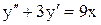
19.
20.
21.
22.
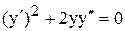
23.
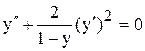
24.
25.

 




⇐ Предыдущая12


Дата добавления: 2015-09-15; просмотров: 440. Нарушение авторских прав; Мы поможем в написании вашей работы!


Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...


ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при ко­торых тело находится под действием заданной системы сил...


Теория усилителей. Схема Основная масса современных аналоговых и аналого-цифровых электронных устройств выполняется на специализированных микросхемах...


Логические цифровые микросхемы Более сложные элементы цифровой схемотехники (триггеры, мультиплексоры, декодеры и т.д.) не имеют...

Понятие массовых мероприятий, их виды Под массовыми мероприятиями следует понимать совокупность действий или явлений социальной жизни с участием большого количества граждан...

Тактика действий нарядов полиции по предупреждению и пресечению правонарушений при проведении массовых мероприятий К особенностям проведения массовых мероприятий и факторам, влияющим на охрану общественного порядка и обеспечение общественной безопасности, можно отнести значительное количество субъектов, принимающих участие в их подготовке и проведении...

Тактические действия нарядов полиции по предупреждению и пресечению групповых нарушений общественного порядка и массовых беспорядков В целях предупреждения разрастания групповых нарушений общественного порядка (далееГНОП) в массовые беспорядки подразделения (наряды) полиции осуществляют следующие мероприятия...

Трамадол (Маброн, Плазадол, Трамал, Трамалин) Групповая принадлежность · Наркотический анальгетик со смешанным механизмом действия, агонист опиоидных рецепторов...

Мелоксикам (Мовалис) Групповая принадлежность · Нестероидное противовоспалительное средство, преимущественно селективный обратимый ингибитор циклооксигеназы (ЦОГ-2)...

Менадиона натрия бисульфит (Викасол) Групповая принадлежность •Синтетический аналог витамина K, жирорастворимый, коагулянт...

Studopedia.info - Студопедия - 2014-2025 год . (0.009 сек.) русская версия | украинская версия