- Що входить до оснастки низу обсадної колони?
- Для чого встановлюють башмак?
- Які є типи зворотних клапанів?
- Яке цементувальне обладнання використовують для цементування нафтових і газових свердловин?
- Які роботи виконують за допомогою цементувальних агрегатів?
Лабораторная работа №7
Исследование полной последовательности цепи переменного тока
Цель: исследование свойств электрических цепей переменного тока; определение параметров активного, реактивного и полного сопротивлений неразветвленной электрической цепи переменного тока; исследование явления резонанса напряжений; построение векторных диаграмм тока и напряжений.
При всяком изменении тока в проводнике электрической цепи магнитное поле, окружающее проводник, будет изменяться.
При пересечении проводника своим же собственным магнитным полем в нем возникает эдс, называемая эдс самоиндукции. Она имеет реактивный характер.
Магнитное поле в катушке создается током  и характеризуется магнитным потоком
и характеризуется магнитным потоком  , который называют потоком самоиндукции.Индуктируемая в катушке эдс
, который называют потоком самоиндукции.Индуктируемая в катушке эдс  определяется по формуле
определяется по формуле
 ,
,
где 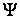 – потокосцепление самоиндукции
– потокосцепление самоиндукции  , Вб;
, Вб;  – количество витков катушки;
– количество витков катушки;  – индуктивность катушки, коэффициент пропорциональности между
– индуктивность катушки, коэффициент пропорциональности между 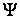 и
и  , Гн.
, Гн.
Знак «минус» в правой части обусловлен законом Ленца, определяющим направление индуктивной эдс: «эдс самоиндукции направлена так, что своим действием препятствует причине, вызвавшей ее появление (т. е. току  )».
)».
Препятствуя изменению тока, эдс самоиндукции  оказывает ему сопротивление, которое называется индуктивным и обозначается
оказывает ему сопротивление, которое называется индуктивным и обозначается  . Формула, определяющая индуктивное сопротивление, Ом, имеет вид
. Формула, определяющая индуктивное сопротивление, Ом, имеет вид 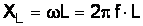 . Напряжение на зажимах катушки при протекании по ней тока
. Напряжение на зажимах катушки при протекании по ней тока  , откуда
, откуда  , где
, где  – индуктивная проводимость
– индуктивная проводимость  , См.
, См.
На рис. 6.2 представлены векторные диаграммы токов и напряжений в индуктивности на обычной координатной плоскости без  (рис. 6.2, а) и при его наличии (рис. 6.2, б). Начальная фаза напряжения больше начальной фазы тока на 90°. Таким образом, в индуктивности ток отстает от напряжения на 90°.
(рис. 6.2, а) и при его наличии (рис. 6.2, б). Начальная фаза напряжения больше начальной фазы тока на 90°. Таким образом, в индуктивности ток отстает от напряжения на 90°.
а б

Рис. 6.2. Векторные диаграммы токов и напряжений в индуктивности: а – на координатной плоскости без  ; б – при его наличии
; б – при его наличии
Система из двух проводящих тел, разделенных диэлектриком, образует конденсатор. Эти проводящие тела называются обкладками конденсатора. Если к ним подключить источник энергии, то на них будет накапливаться заряд  , пропорциональный напряжению на конденсаторе:
, пропорциональный напряжению на конденсаторе:  :
:  . Коэффициент пропорциональности С между
. Коэффициент пропорциональности С между  и
и  называется емкостью конденсатора.
называется емкостью конденсатора.
Емкостная проводимость  . Величина, обратная емкостной проводимости, называется емкостным сопротивлением
. Величина, обратная емкостной проводимости, называется емкостным сопротивлением 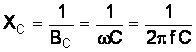 . Величина тока
. Величина тока  , отсюда
, отсюда  .
.
На рис. 6.3 представлены векторные диаграммы токов и напряжений в емкости на координатной плоскости без  (рис. 6.3, а) и при его наличии (рис. 6.3, б). Таким образом, в емкости ток опережает напряжение на 90°.
(рис. 6.3, а) и при его наличии (рис. 6.3, б). Таким образом, в емкости ток опережает напряжение на 90°.
а б

Рис. 6.3. Векторные диаграммы токов и напряжений в емкости: а – на координатной плоскости без  ; б – при его наличии
; б – при его наличии
Определение тока в цепи и напряжений на ее элементах можно выполнить на основе векторной диаграммы.
В последовательной цепи (рис. 6.4, а) общим для всех элементов является протекающий по ним ток. С него начинаем построение векторной диаграммы последовательной электрической цепи. На рис. 6.4, б изображается вектор тока горизонтально. Далее строятся векторы напряжений на всех элементах. В соответствии со вторым законом Кирхгофа вектор входного напряжения  . Сложение векторов выполняется по правилу многоугольника, когда каждый последующий вектор пристраивается к концу предыдущего.
. Сложение векторов выполняется по правилу многоугольника, когда каждый последующий вектор пристраивается к концу предыдущего.
а б

Рис. 6.4. Неразветвленная электрическая цепь переменного тока: а – схема последовательного соединения R, L и C элементов; б – векторная диаграмма
Известно, что напряжение на активном сопротивлении  совпадает по фазе с током, поэтому вектор
совпадает по фазе с током, поэтому вектор  направлен по вектору тока
направлен по вектору тока  . К его концу пристраиваем вектор
. К его концу пристраиваем вектор  и направляем его вверх под углом
и направляем его вверх под углом  , так как напряжение на индуктивности
, так как напряжение на индуктивности  опережает ток на
опережает ток на  . Напряжение на емкости
. Напряжение на емкости  находится в противофазе с
находится в противофазе с  , т. е. отстает от тока на
, т. е. отстает от тока на  , поэтому вектор
, поэтому вектор 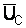 , пристроенный к концу вектора
, пристроенный к концу вектора  , направлен вниз. Сумма векторов
, направлен вниз. Сумма векторов  дает вектор напряжения
дает вектор напряжения  .
.
Величины напряжений на отдельных элементах цепи определяются по закону Ома:  ,
,  ,
,  .
.
Согласно теореме Пифагора из треугольника oab определяется
 ,
,
где 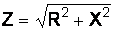 – полное сопротивление цепи, Ом;
– полное сопротивление цепи, Ом; 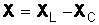 – общее реактивное сопротивление, Ом.
– общее реактивное сопротивление, Ом.
Закон Ома для всей цепи:  , где
, где  – полная проводимость цепи, См.
– полная проводимость цепи, См.
Угол сдвига фаз  между напряжением
между напряжением  и током
и током  определяется из треугольника напряжений oabили треугольника сопротивлений:
определяется из треугольника напряжений oabили треугольника сопротивлений:
 .
.
Для вычисления мощностей, потребляемых цепью из сети, используем формулы, выведенные из закона Джоуля–Ленца: 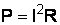 – активная мощность, Вт;
– активная мощность, Вт; 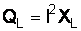 – реактивная индуктивная мощность, вар;
– реактивная индуктивная мощность, вар;  – реактивная емкостная мощность, вар;
– реактивная емкостная мощность, вар;  – общая реактивная мощность, вар;
– общая реактивная мощность, вар;  – полная мощность электрической цепи переменного тока, ВА.
– полная мощность электрической цепи переменного тока, ВА.
Режим, когда в цепи, содержащей последовательно соединенные активное сопротивление, индуктивность и емкость, ток совпадает по фазе с напряжением, называют резонансом напряжения. Это означает, что входное реактивное сопротивление в цепи равно нулю:  , или
, или  . В этом случае
. В этом случае  , и цепь носит чисто активный характер, т. е.
, и цепь носит чисто активный характер, т. е.  , и сдвиг фаз отсутствует (
, и сдвиг фаз отсутствует (  ).
).
Так как при резонансе  , то соответственно
, то соответственно  .
.
Напряжения на индуктивности и емкости в этом режиме равны по величине и, находясь в противофазе, компенсируют друг друга (рис. 6.5). Все приложенное к цепи напряжение приходится на ее активное сопротивление.
Напряжение на индуктивности и емкости может значительно превышать напряжение на входе цепи. Их отношение, называемое добротностью контура  , определяется величинами индуктивного (или емкостного) и активного сопротивлений: , определяется величинами индуктивного (или емкостного) и активного сопротивлений:
 .
Добротность показывает, во сколько раз напряжения на индуктивности и емкости при резонансе превышают напряжение, приложенное к цепи.
Резонанса можно достичь, изменяя любой из параметров – частоту, индуктивность, емкость. При этом меняются реактивное и полное сопротивления цепи, а вследствие этого – ток, напряжения на элементах и сдвиг фаз. .
Добротность показывает, во сколько раз напряжения на индуктивности и емкости при резонансе превышают напряжение, приложенное к цепи.
Резонанса можно достичь, изменяя любой из параметров – частоту, индуктивность, емкость. При этом меняются реактивное и полное сопротивления цепи, а вследствие этого – ток, напряжения на элементах и сдвиг фаз.
| 
|
Емкость  , при которой наступает резонанс, можно определить из формулы
, при которой наступает резонанс, можно определить из формулы
 .
.
При резонансе  , или
, или  , откуда
, откуда  , где
, где
 – собственная частота колебания контура. Таким образом, при резонансе напряжений частота
– собственная частота колебания контура. Таким образом, при резонансе напряжений частота  источника напряжения равна собственной частоте
источника напряжения равна собственной частоте  колебания контура.
колебания контура.
При резонансе напряжения  . Величина
. Величина  называется волновым сопротивлением контура.
называется волновым сопротивлением контура.
Тогда добротность  .
.

 и характеризуется магнитным потоком
и характеризуется магнитным потоком  , который называют потоком самоиндукции.Индуктируемая в катушке эдс
, который называют потоком самоиндукции.Индуктируемая в катушке эдс  определяется по формуле
определяется по формуле ,
,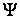 – потокосцепление самоиндукции
– потокосцепление самоиндукции  , Вб;
, Вб;  – количество витков катушки;
– количество витков катушки;  – индуктивность катушки, коэффициент пропорциональности между
– индуктивность катушки, коэффициент пропорциональности между  оказывает ему сопротивление, которое называется индуктивным и обозначается
оказывает ему сопротивление, которое называется индуктивным и обозначается  . Формула, определяющая индуктивное сопротивление, Ом, имеет вид
. Формула, определяющая индуктивное сопротивление, Ом, имеет вид 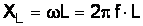 . Напряжение на зажимах катушки при протекании по ней тока
. Напряжение на зажимах катушки при протекании по ней тока  , откуда
, откуда  , где
, где  – индуктивная проводимость
– индуктивная проводимость  , См.
, См. (рис. 6.2, а) и при его наличии (рис. 6.2, б). Начальная фаза напряжения больше начальной фазы тока на 90°. Таким образом, в индуктивности ток отстает от напряжения на 90°.
(рис. 6.2, а) и при его наличии (рис. 6.2, б). Начальная фаза напряжения больше начальной фазы тока на 90°. Таким образом, в индуктивности ток отстает от напряжения на 90°.
 ; б – при его наличии
; б – при его наличии , пропорциональный напряжению на конденсаторе:
, пропорциональный напряжению на конденсаторе:  :
:  . Коэффициент пропорциональности С между
. Коэффициент пропорциональности С между  . Величина, обратная емкостной проводимости, называется емкостным сопротивлением
. Величина, обратная емкостной проводимости, называется емкостным сопротивлением 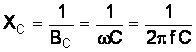 . Величина тока
. Величина тока  , отсюда
, отсюда  .
. (рис. 6.3, а) и при его наличии (рис. 6.3, б). Таким образом, в емкости ток опережает напряжение на 90°.
(рис. 6.3, а) и при его наличии (рис. 6.3, б). Таким образом, в емкости ток опережает напряжение на 90°.
 ; б – при его наличии
; б – при его наличии . Сложение векторов выполняется по правилу многоугольника, когда каждый последующий вектор пристраивается к концу предыдущего.
. Сложение векторов выполняется по правилу многоугольника, когда каждый последующий вектор пристраивается к концу предыдущего.
 совпадает по фазе с током, поэтому вектор
совпадает по фазе с током, поэтому вектор  направлен по вектору тока
направлен по вектору тока  . К его концу пристраиваем вектор
. К его концу пристраиваем вектор  и направляем его вверх под углом
и направляем его вверх под углом  , так как напряжение на индуктивности
, так как напряжение на индуктивности  опережает ток на
опережает ток на  находится в противофазе с
находится в противофазе с 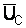 , пристроенный к концу вектора
, пристроенный к концу вектора  дает вектор напряжения
дает вектор напряжения  .
. ,
,  ,
,  .
. ,
,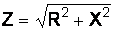 – полное сопротивление цепи, Ом;
– полное сопротивление цепи, Ом; 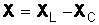 – общее реактивное сопротивление, Ом.
– общее реактивное сопротивление, Ом. , где
, где  – полная проводимость цепи, См.
– полная проводимость цепи, См. между напряжением
между напряжением  и током
и током  определяется из треугольника напряжений oabили треугольника сопротивлений:
определяется из треугольника напряжений oabили треугольника сопротивлений: .
.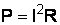 – активная мощность, Вт;
– активная мощность, Вт; 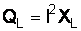 – реактивная индуктивная мощность, вар;
– реактивная индуктивная мощность, вар;  – реактивная емкостная мощность, вар;
– реактивная емкостная мощность, вар;  – общая реактивная мощность, вар;
– общая реактивная мощность, вар;  – полная мощность электрической цепи переменного тока, ВА.
– полная мощность электрической цепи переменного тока, ВА. , или
, или  . В этом случае
. В этом случае  , и цепь носит чисто активный характер, т. е.
, и цепь носит чисто активный характер, т. е.  , и сдвиг фаз отсутствует (
, и сдвиг фаз отсутствует (  ).
). , то соответственно
, то соответственно  .
. .
Добротность показывает, во сколько раз напряжения на индуктивности и емкости при резонансе превышают напряжение, приложенное к цепи.
Резонанса можно достичь, изменяя любой из параметров – частоту, индуктивность, емкость. При этом меняются реактивное и полное сопротивления цепи, а вследствие этого – ток, напряжения на элементах и сдвиг фаз.
.
Добротность показывает, во сколько раз напряжения на индуктивности и емкости при резонансе превышают напряжение, приложенное к цепи.
Резонанса можно достичь, изменяя любой из параметров – частоту, индуктивность, емкость. При этом меняются реактивное и полное сопротивления цепи, а вследствие этого – ток, напряжения на элементах и сдвиг фаз.

 , при которой наступает резонанс, можно определить из формулы
, при которой наступает резонанс, можно определить из формулы .
. , откуда
, откуда  , где
, где  – собственная частота колебания контура. Таким образом, при резонансе напряжений частота
– собственная частота колебания контура. Таким образом, при резонансе напряжений частота  источника напряжения равна собственной частоте
источника напряжения равна собственной частоте  . Величина
. Величина  называется волновым сопротивлением контура.
называется волновым сопротивлением контура.  .
.


