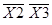Наборы, не отмеченные в таблице, являются простыми импликантами.

Аналогично проведем следующий этап упрощения полученного в таблице результата, объединяя только те члены, у которых прочерк стоит в одном и том же разряде. Результаты сравнения представлены в табл.4.14. В этой таблице одинаковые члены можно вычеркнуть, после чего дальнейшее упрощение невозможно. В таблице остались не вычеркнутыми только простые импликанты.

Для того, чтобы выбрать минимальную форму записи, состоящую из простых импликант, необходимо построить таблицу простых импликант (табл.4.15). Если какая-либо из найденных простых импликант содержится в одном или нескольких единичных наборах, то в соответствующей клетке ставится крест. Таким образом проверяются все простые импликанты.

В табл.4.15 выбирают столбцы, содержащие только один крест.

Таблица 4.13

Сравниваемые наборы	X1	X2	X3	X4
0,1 0,2 0,4 0,8	-	-	-	-
1,3			-
1,9	-
2,3				-
2,6		-
4,6			-
8,9				-
3,7		-
3,11	-
6,7				-
9,11			-
7,15	-
11,15		-

 

Простые импликанты, соответствующие столбцам с одним крестом, должны обязательно входить в минимальную ДНФ.

Столбцы, в которые попадают кресты из строк обязательных импликант можно вычеркнуть.

Если останутся невычеркнутые столбцы, то необходимо в группу обязательных импликант включить одну или несколько простых импликант, таких, которые позволили бы вычеркнуть все оставшиеся столбцы.

В рассматриваемом примере минимальная ДНФ для заданной функции имеет вид

Таблица 4.14

Сравниваемые наборы	X1	X2	X3	X4
0,1;2,3 0,1;8,9 0,2;1,3 0,2;4,6 0,4;2,6 0,8;1,9	- -	- -	- - - -	- - - -
1,3;9,11	-		-
1,9;3,11	-		-
2,3;6,7		-		-
2,6;3,7		-		-
3,7;11,15	-	-
3,11;7,15	-	-

 

Таблица 4.15

Простые импликанты	Единичные наборы заданной функции
X1X2X3X4	X1X2X3X4	X1X2X3X4	X1X2X3X4	X1X2X3X4	X1X2X3X4	X1X2X3X4	X1X2X3X4	X1X2X3X4	X1X2X3X4	X1X2X3X4
	+	+	+			+
	+	+						+
	+		+				+
		+				+		+		+
			+			+	+		+
						+			+	+

 

В методе Квайна--Мак-Класки наиболее ценным является второй этап - нахождение простых импликант при помощи таблицы Квайна-Мак-Класки. Существенными преимуществами такой таблицы являются большая наглядность, сравнительная простота, надежность контроля. В целом этот метод минимизации целесообразно применять к функциям не более, чем 6-7 переменных.

При применении метода Квайна-Мак-Класки для получения минимальной конъюнктивной нормальной формы (МКНФ) функции алгебры логики имеются следующие особенности:

‑ пары склеиваемых членов имеют вид

‑ члены КСНФ представляют собой дизъюнкции переменных, которые имеют инверсные значения по сравнению с их значениями в наборах, на которых функция равна 0.

 

 

3. Задание

 

1) Изучить теоретический материал.

3) Минимизировать функцию, заданную числовым набором, методом Квайна-Мак-Класки. Сравнить полученные выражения с остльными методами минимизации.. Вариант выбирается из таблицы 4.16 по указанию преподавателя.

4) Построить схему, реализующую минимизированную функцию, на логических элементах.

Таблица 4.16

№ варианта	Функция F(X1,X2,X3.X4)	№ варианта	Функция F(X1,X2,X3.X4)
	2,4,5,7,10,14 0,2,5,11,14,15 1,5,6,8,11,13 3,4,7,11,12,15 2,4,6,9,11,15 2,3,8,12,13,14 4,5,8,10,11,13 0,1,3,4,9,14 8,9,11,10,13,15 5,7,8,9,11,15 5,10,12,13,14 1,4,5,6,7,8,9,12,13 3,4,5,7,9,13,14,15 0,1,2,3,4,6,7,8,9,11,15		3,5,7,9,11,13,14 1,3,4,6,9,11,13 1,2,3,5,7,8,10 1,3,7,8,9,11 3,5,8,8,11,12,13 0,2,4,8,9,10,11,13 1,2,3,6,9,11,12 3,4,5,7,9,11,12,14 1,6,7,8,11,14,15 2,3,5,7,9,10,11,15 3,5,6,8,9,11,12,14 1,3,5,7,8,10,11 0,3,4,5,7,11,13 0,2,6,8,10,11,15

 

 

4. Содержание отчета

 

1) Аналитическое выражение для заданной функции.

2) Минимизация функции методом Квайна-Мак-Класки.

3) Аналитические выражения для минимизированной функции.

4) Схема, реализующая минимизированную функцию, на логических элементах. Ее таблица истинности.

5) Описание последовательности построения моделируемых схем.

6) Краткие выводы.

 

Контрольные вопросы

 

1) Что такое ДСНФ?

2) Что такое КСНФ?

3) Что такое сокращенная ДНФ?

4) Что такое тупиковая ДНФ?

5) Что такое импликанта?

6) Что такое простая импликанта?

7) Что такое вес кода?

8) Какие наборы являются соседними?