Лабораторна робота №4. Таблиця 4.1. Експерементальні дані Вимір. В-ни Витрат початкової суміші, GF Витрати дистиляту, Gp Витрата флегми, Gф Склад
Таблиця 4.1. Експерементальні дані
Обробка результатів Запишемо рівняння матеріального балансу ректифікаційної колони:
З рівняння (4.1.) знайдемо масу кубового залишку
Звідси З рівняння (4.2.) знаходимо
Розрахуємо мольні долі для кожної суміші за формулою
Отже, маємо:
Знайдемо флегмове число за формулою
Щоб побудувати графік для визначення числа ступенів зміни концентрації(теоретичних тарілок),знайдемо величину В, що дорівнює:
Побудувавши графік та визначивши число теоретичних тарілок, знайдемо коефіцієнт збагачення чи так званого ККД тарілок
Висновок На цій лабораторній роботі ми вивчили будову ректифікаційної колони, процес ректифікації; його основні параметри: число ступенів зміни концентрації (теоретичних тарілок) та коефіцієнт збагачення встановлених в колоні ситчастіх тарілок, який дорівнює Лабораторна робота №4 На тему: «Символьні перетворення в середовищі MathCad»
Мета: набути навичок при виконанні символьних обчислень та навчитися будувати графіки різних типів у MathCad.
Завдання.
1. Обчислити заданий вираз з заданою точністю
2. Вивести наступні числа в комплексній формі
3. Спростити даний вираз
4. Даний вираз
4.1. розкласти на множники 4.2. для отриманого виразу розкрити дужки і привести подібні 4.3. підставити у вираз (1) 4.4. для отриманого виразу привести подібні по змінній 4.5. отримати коефіцієнти полінома для виразу (1) 5. Розкласти вираз на елементарні дроби
6. Розкласти функцію
Символьні обчислення в середовищі MathCad можна здійснювати за допомогою - команд меню; - за допомогою оператора символьного виводу → та ключових слів символьного процесора та звичайних формул. Для символьних обчислень за допомогою команд використовується команда головного меню Символика (Symbolics) рис.3.1, що об’єднує математичні операції, які MathCad вміє виконувати аналітично. Для реалізації другого варіанту використовується спеціальна математична панель інструментів рис.3.2, яка викликається натисненням на кнопку
Рис. 3.1 Рис. 3.2
|

 (4.1)
(4.1) (4.2)
(4.2) :
: , де
, де знаходимо з загальної формули
знаходимо з загальної формули  ,тобто
,тобто г
г г
г г.
г. г.
г. ,вважаючи
,вважаючи  та
та  :
: г
г (4.3)
(4.3)


 . Отже, маємо:
. Отже, маємо:

 за формулою:
за формулою:
 (п’ять знаків після коми)
(п’ять знаків після коми)


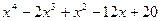 (1)
(1)
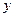

 в ряд із заданою точністю
в ряд із заданою точністю 

 .
.




