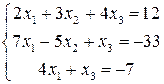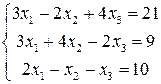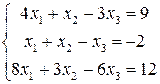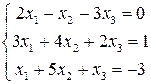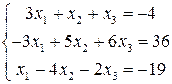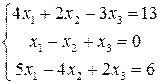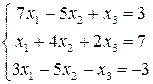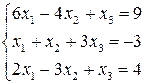Розв’язування типового варіанта
1. Маємо систему лінійних неоднорідних алгебраїчних рівнянь:
Необхідно: Перевірити, чи є система сумісною, та в разі сумісності розв’язати її: а) за формулами Крамера; б) за допомогою оберненої матриці (матричним методом);
Розв’язання: Сумісність даної системи перевіримо за теоремою Кронекера-Капеллі. За допомогою елементарних перетворювань знайдемо ранг матриці та ранг розширеної матриці Для цього помножимо перший рядок матриці В на –2 та додамо до другого, далі множимо перший рядок на –3 і додаємо до третього, змінюємо третій і другий стовпці місцями:
Отже а) за формулами Крамера: якщо
знаходимо: б) Для знаходження розв’язку системи за допомогою оберненої матриці запишемо систему рівнянь у матричної формі
Розв’язок системи у матричної формі має вигляд Знаходимо обернену матрицю
Розв’язок системи:
Отже, 2. Розв’язати однорідну систему лінійних алгебраїчних рівнянь:
Розв’язання: Визначник системи 3. Розв’язати однорідну систему лінійних алгебраїчних рівнянь:
Через те, що визначник системи Маємо:
Через те, що визначник з коефіцієнтів при невідомих
Розв’язуємо останню систему за формулами Крамера:
Звідси знаходимо: Вважаючи, наприклад, . 2. Варіанти індивідуальних завдань.
Задача №1. Задана неоднорідна система лінійних рівнянь. Необхідно: а) перевірити її сумісність; б) у випадку сумісності розв’язати систему трьома засобами: - за формулами Крамера; - за допомогою оберненої матриці.
Задача №2. Розв’язати однорідну систему лінійних рівнянь:
|


 даної системи
даної системи .
. ~
~ 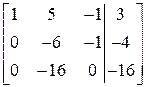 ~
~ 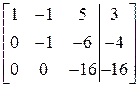
 . Тоді за теоремою Кронекера-Капеллі випливає сумісність даної системи.
. Тоді за теоремою Кронекера-Капеллі випливає сумісність даної системи. ,
,  ,
,  ,
,  , де
, де ,
,  ,
, 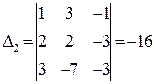 ,
, 
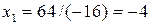 ,
,  ,
, 
 , де
, де ,
,  ,
,  .
.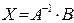 .
. (вона існує, тому що
(вона існує, тому що  ):
):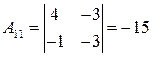 ,
,  ,
, 
 ,
,  ,
, 
 ,
,  ,
, 


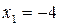 ,
,  ,
, 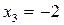

 , тому система має єдиний нульовий розв’язок:
, тому система має єдиний нульовий розв’язок: 
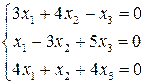
 , то система має нескінченну множину розв’язків. Оскільки
, то система має нескінченну множину розв’язків. Оскільки  , візьмемо будь-які два рівняння системи (наприклад, перше і друге) і знайдемо її розв’язок.
, візьмемо будь-які два рівняння системи (наприклад, перше і друге) і знайдемо її розв’язок.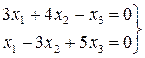
 і
і  не дорівнює нулю, то в якості базисних невідомих візьмемо
не дорівнює нулю, то в якості базисних невідомих візьмемо 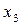 в праві частини рівнянь:
в праві частини рівнянь:
 ,
,  , де
, де ,
,  ,
, 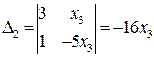
 ,
,  .
. , де k ÎR – довільний коефіцієнт пропорційності, одержуємо розв’язок вихідної системи:
, де k ÎR – довільний коефіцієнт пропорційності, одержуємо розв’язок вихідної системи: 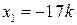 ,
,  ,
,  .
.