Цели и задачи контрольной работы
Лабораторна робота № 1. Підбір інструменту при визначенні густини тіл правильної геометричної форми. Прилади та приладдя: вимірювані тіла, штангенциркуль, мікрометр,технічні терези, різноваги. Мета роботи: засвоїти методику підбору та використання інструментів в непрямих вимірах.
Коротка теорія та метод вимірювання
Густиною однорідного тіла називається маса одиниці об’єму тіла або відношення маси тіла до його об’єму: ρ = m / V. (1) Масу тіла можна визначити зважуванням, об’єм тіла правильної геометричної форми визначають шляхом вимірювань їх геометричних розмірів та наступних обчислень. В даній роботі визначають об’єми циліндра і паралелепіпеда відповідно за формулами: V = hπd2/4; V = lbh, (2) де: l – довжина, b – ширина, h – висота паралелепіпеда; h – висота циліндра, d- діаметр циліндра знаходять за прямими вимірюваннями. Вибір інструменту чи приладу для кожного вимірювання визначається необхідною точністю відшукуваних величин. Нехай при визначенні густини циліндричного тіла одержали при вимірюваннях: h = 50,00 ± 0,05мм, d =10,00 ± 0,005мм, m = 5,000 ± 0,005г, де похибка вимірювань геометричних розмірів в 0,05мм є мінімальною при використанні штангенциркуля з ціною поділки 0,1мм, а похибка 0,005г – мінімальна при використанні різноваги 0,01г. Відносні похибки вимірювань h, d і m відповідно дорівнюють εh = 0,001, εd = 0,005, εm = 0,001. Якщо знайти відносну похибку вимірювань густини за співвідношенням (18) із п. 6.6., то одержимо: ε = [(Δh / h) + (Δd / d) + (Δm / m) ]1/2= (0,001 + 0,010 + 0,001)1/2 = 0,010 (3) Замінимо при вимірюванні діаметра циліндра штангенциркуль на мікрометр. Найменша ціна поділки мікрометра 0,01 мм. Відносна похибка визначення діаметра буде становити Δd / d = 0,0005. Тоді відносна похибка визначення густини буде складати: ε = [(0,001 + 0,001 + (0,0010)]1/2 = 0,002 Отже, при виконанні непрямих вимірів треба підбирати таких комплекс вимірювальних приладів та інструментів, який дозволив би одержати приблизно однакові відносні похибки вимірювань окремих величин, що входять в розрахункову формулу. В наведеному кінцевому прикладі похибки вимірювань окремих величин роблять однаковий внесок у відносну похибку вимірювань густини.
Порядок виконання роботи:
1. Визначити масу тіла шляхом зважування. 2. Підібрати інструмент для виміру лінійних розмірів тіл. 3. Виконати вимірювання геометричних розмірів в трьох місцях для кожного тіла. 4. Визначити середньоквадратичне відхилення середньоарифметичного кожного виміру від істинного згідно з п.4.6.8. Довірчий інтервал для кожного виміру взяти для довірчої ймовірності 0,7, тобто Δh = 1,3 S(<g>)), Δd = 1,3 S(<g>), Δm = 1,3 S(<g>) і т. д. 5. Обчислити густину тіл по середніх значеннях виміряних величин. 6. Обчислити відносні похибки визначення густини для двох тіл за формулами: для циліндра – ε = [(Δh / h)2 + 2(Δd / d)2 + (Δm / m)2 ]1/2; для паралелепіпеда - ε = [(Δl / l)2 + (Δb / b)2 + (Δh / h)2 + (Δm / m)2 ]1/2. При вимірюваннях маси тіла, як правило одержують три однакові значення, тому за Δm має бути прийняте значення 0,005 г, що дорівнює половині маси найменшої різноваги. 6. Обчислити довірчі інтервали визначення густини тіл шляхом множення середніх значень густин на відносні похибки їх визначення. Результати вимірювань і розрахунків занести до таблиці (геометричні розміри –см, маса – г, густина – г/ см3 ).
Таблиця 1. Визначення густини циліндричного тіла
Таблиця 2. Визначення густини тіла - паралелепіпеда
Дайте відповідь на запитання:
1. Якими інструментами мають вимірюватись: • пластинка 90 мм х 60 мм х 10 мм? • шина 940 мм х 70 мм х 10 мм? 2. Як перевести одержані в роботі значення густини в одиниці системи SI? 3. Чи достатньо точності одного штангенциркуля для виконання вимірювань, якщо абсолютна похибка визначення маси дорівнює 0,05 г?
Лабораторна робота №2. Визначення питомої ваги твердого тіла зважуванням в двох середовищах. Прилади та приладдя: гідростатичні терези з різновагами, досліджувані тіла, склянка з водою і спиртом. Мета роботи: засвоїти метод визначення питомої ваги тіл неправильної геометричної форми.
Коротка теорія
Питомою вагою однорідного тіла називають вагу одиниці об’єму тіла або відношення ваги тіла P до його об’єму V: d = P / V (1) Вагу тіла можна визначити як добуток маси тіла на прискорення вільного падіння в даному місці Землі. Масу тіла при цьому визначають зважуванням на важільних терезах. За законом Архімеда на тіло, занурене в рідину або газ, діє виштовхувальна сила, що дорівнює вазі рідини або газу, що витіснило тіло. В роботі визначається питома вага тіла з високою порівняно з повітрям густиною, тому вага тіла в повітрі практично дорівнює його вазі в вакуумі P. Якщо зважити тіло в деякий рідині, питома вага якої dp відома, то вага його виявиться рівною: Pp = P – dp V, (2) де V - об’єм зануреного тіла. Визначаючи із (2) об’єм тіла V і підставляючи його в (1), знаходимо питому вагу тіла: d = P dp / (P – Pp), (3) Порядок виконання роботи:
1. Зважити тіло в повітрі, у воді і в спирті. Результати зважування та густину середовищ занести в таблицю. 2. Розрахувати питому вагу тіла за (3) для випадку води і спирту. 3. Для знайдених двох значень питомої ваги. розрахувати довірчий інтервал визначення питомої ваги для надійності 0,7. 4. Подати результати в вигляді d = < d > ± Δd.
Дайте відповідь на запитання:
1. Як пов’язані між собою питома вага та густина? 2. Густину яких тіл можна визначити вивченим методом? 3. Як визначити за питомою вагою сплаву співвідношення двох компонентів?
Лабораторна робота №3. Визначення швидкості та пробивної здатності кулі за допомогою обертового барабана. Прилади та приладдя: вимірювальна установка, що складається з пневматичної рушниці, барабана на осі мотора і з тахометра, штангенциркуль, кулі, стрічка з міліметрового паперу, картонна пластина. Мета роботи: засвоїти один з методів вивчення частинок, що рухаються.
Коротка теорія та метод вимірювання
З пневматичної рушниці роблять постріл в паперову стрічку, що натягнена на барабан. Якщо барабан нерухомий, то постріл відбувається в точках 0-0, відстань між якими по дузі кола барабана дорівнює L0 (рис. 1). Доки куля, що летить вздовж хорди зі швидкістю v, пролітає хорду за проміжок часу Δt: Δt = a / v, (1) барабан, обертаючись з кутовою швидкостю ω, повертається на кут Δφ = ωΔt. Враховуючи, що кут повороту дорівнює відношенню шляху ΔL, який точки проходять по колу барабана, до радіуса барабана R, а також приймаючи до уваги (1), знаходимо: v = R ω a / ΔL, (2) Довжина хорди a = 2 R sin (φ / 2), тому з (2) остаточно одержуємо: v = Вимірявши величину R, ω, L0, ΔL за (3) обчислюємо швидкість кулі, а потім розраховуємо кінетичну енергію: W0 = m v2 / 2, (4) Поставимо на шляху кулі перед барабаном перепону у вигляді картонного аркушу. Тоді на пробивання аркушу буде потрачена енергія, так що швидкість кулі зменшиться і збільшиться відстань між точками прострілу ΔL. Вимірявши величину ΔL, за (2) обчислюємо нову швидкість кулі v΄, а потім роботу пробивання перепони: A = W0 - W΄ = де F - середня сила опору; b - товщина картону. Вважаючи силу опору при пробою картону сталою та вимірявши товшину картону, визначимо пробивну здатність кулі в подібному картоні до її повної зупинки, коли W΄= 0: b0 = W0 b / A (6)
Порядок виконання роботи:
1. Ознайомитись з установкою. 2. Відгвинтити затискачі на барабані та встановити паперову стрічку, намотуючи її за годинниковою стрілкою. Ретельно закріпити затискачі. 3. Виміряти діаметр барабана штангенциркулем. 4. Закрити охоронну кришку та зарядити рушницю. 5. Ввімкнути електромотор і після усталення швидкості обертання зробити постріл. Визначити за тахометром число обертів ni в секунду і вимкнути двигун. Кутова швидкість обертання барабана дорівнює ωi = 2π ni. 6. Відчинити кришку, відмітити цифрами 1 - 1 точки прострілу та виміряти відстань L1 між ними. 7.Зачинити кришку, виміряти товщину b пробиваної пластинки, вставити її в проріз кришки, зарядити рушницю, ввімкнути електромотор, визначити за тахометром усталене число обертів n2, зробити постріл і вимкнути двигун. 8. Відчинити кришку, відмітити точки прострілу 2-2 і виміряти відстань L2 між ними. Зачинити кришку. 9. Зробити постріл при нерухомому барабані, відчинити кришку і виміряти довжину дуги L0. Обчислити кут φ / 2 = L0 / R і знайти його синус. 10. Визначити ΔL = L1 – L0, ΔL΄ = L2 – L0 і виконати розрахунки за запропонованими співвідношеннями, приймаючи масу кулі m = 280 мг. 11. Результати розрахунків подати в таблиці:
Таблиця 1. Визначення швидкості та пробивної здатності кулі.
Зняти стрічку з барабана і поставити затискачі на місце. Стрічку підписати і прикласти до звіту. У звіті подати приклад розрахунків.
Дайте відповідь на запитання:
1. Як треба змінити умови вимірювань, якщо швидкість кулі збільшилась б в 5 разів? 2. Якою має бути швидкість кулі, щоб вхідний і вихідний отвори пробою співпадали?
Лабораторна робота № 4. Дослідження сил тертя за допомогою плоского трибометра. Прилади та приладдя: плоский трибометр зі змінними пластинами і набори тіл із різних металів, різноваги. Мета роботи: засвоїти один із методів визначення коєфіцієнта тертя ковзання.
Коротка теорія та метод вимірювання
Розрізняють два основні види тертя: внутрішне і зовнішнє. Внутрішнє тертя в твердих, аморфних тілах та рідинах має складний механізм, пов’язаний з деформацією. В твердих тілах внутрішнє тертя призводить до нагрівання деформованого тіла. В рідинах та газах воно проявляється як в’язкість – опір відносному переміщенню різних шарів речовини. Зовнішне тертя – це протидія відносному переміщенню прилягаючих тіл. Сила протидії спрямована вздовж стичних поверхонь. Ми будемо вивчати зовнішнє тертя. Згідно закону Амонтона –Кулона сила зовнішнього тертя пропорційна силі нормальної реакції N між стичними тілами і не залежить від величини стичної поверхні тіл і швидкості їх відносного руху: F = k N (1) Коефіцієнт тертя k залежить від матеріалу тіл, що труться, якості обробки поверхонь, наявності на поверхнях забруднень або мастила. Закон (1) наближений і застосовується тільки для орієнтовних розрахунків. В дійсності явище тертя значно складніше: мають бути враховані сили міжмолекулярного зчеплення, величина стичних поверхонь, врешті закон (1) не враховує залежність сил тертя від швидкості відносного руху тіл, що труться, тобто не відрізняє статичне і кінематичне тертя. Статичне тертя - це тертя між тілами, що знаходяться в стані спокою: при малих значеннях діючої на тіло сили воно залишається в спокою по відношенню до поверхні іншого тіла із-за наявності сили тертя спокою. Згідно з третім законом механіки сила тертя дорівнює за величиною і протилежна за напрямком прикладеній силі. При деякому максимальному значенні прикладеної сили тіло зривається з місця і починає рухатись. Така властивість сил статичного тертя називається застоєм. Причина статичного тертя - наявність сил молекулярного зчеплення і зачеплення нерівностей поверхонь тіл. Після того, як тіло почало рухатись, статичне тертя змінюється кінематичним, причому величина сили кінематичного тертя виявляється меншою за максимальну силу тертя спокою. Кінематичне тертя зумовлене рядом причин, на яких ми зупинятися не будемо. На сьогодні “точного” закону тертя не існує, тому на практиці коефіцієнт тертя визначають для різних пар тертьових матеріалів при різній якості обробки поверхонь, різних тисках і швидкостях руху, а результати подають у вигляді довідкових таблиць. В даній роботі для вимірювання сил тертя застосовується плоский трибометр з набором пластин і тіл із різних матеріалів. Трибометр - це площина, кут нахилу якої до горизонту можна змінювати. Трибометр має градусну шкалу, затискач для фіксування кута нахилу, нерухомий блок для нитки і шальку для встановлення гир. Зовнішньо рушійною силою в такому трибометрі є сила натягу нитки, паралельна похилій площині, що визначається вагою гир, складової сили тяжіння тіла, паралельно похилій площині, а також силою тертя. Величину рушійної сили можна регулювати підбором маси гир і зміною кута нахилу площини трибометра. Застій долається легкими ударами молоточка по пластині. Розглянемо рух тіла на похилій площині під дією вказаних сил. Розкладено силу тяжіння P, що діє на тіло, на дві складові – паралельну похилій площині (складова P1) і перпендикулярну їй (складова P2). Складова P2 викликає з боку похилої площини рівновелику собі силу нормальної реакції N. В залежності від того, куди спрямована рівнодіюча всіх сил, прикладених до тіла, в тому напрямку буде прискорюватись тіло. Хай сила натягу нитки F΄ не менша від суми сили тертя F1 і складової P1 (рис. 1а). Тоді тіло рухається з прискоренням вгору. Якщо складова P1 більша за суму сили натяг F΄ у нитки та силу тертя F2, то тіло буде рухатись з прискоренням вниз (рис. 1б). При рівномірному ковзанні тіла вгору має виконуватись:
F΄ = P1 + F1. (2)
У співвідношенні (2) сила тертя F1 = kN = Pcosα, а складова P1 = Psinα. Підставляючи F1 і P1 в (2), знаходимо коефіцієнт тертя:
k1 = F΄/ P cos (α1) – tg (α1). (3)
При рівномірному русі тіла вниз по похилій площені виконується рівність: P1 = F΄ + F2. (4) Після підстановки в (4) значень P1 і F2 для коефіцієнта тертя одержуємо
k2 = tg (α2) - F΄/ (P cos (α2). (5)
З метою зменшення похибок, зумовлених різними значеннями сил нормального тиску та різного значення величини молекулярного зчеплення, за коефіцієнт тертя приймають половину суми (3) і (5): k = (k1 + k2 )/2. (6) У випадку найпростіших (грубих вимірювань) коефіцієнт тертя визначають без врахування додаткової сили F΄. При цьому підбирають такий кут α3, при якому тіло рівномірно ковзає по похилій площині. В цьому разі співвідношення (5) приводить до k 3 = tg (α3). (7)
а б Рис. 1.
Порядок виконання роботи:
1. За пропозицією викладача відібрати пластину та два тіла: 1 – сталь 3; 2 - антикорозійна сталь; 3 – латунь; 4 – дюраль. 2. Ретельно очистити крейдою поліровані поверхні до рівномірного блиску та зібрати ганчіркою залишки порошку з поверхні тіл. 3. Вставити пластинку на трибометр, фіксуючи її кінцевими стопорами через отвори. 4. Визначити вагу тіла -P з точністю до 5 г. Відпустити затискач, підійняти площину в верхнє положення і затиснути. Покласти тіло на площину, причепити до нього за гачок нитку з шалькою і покласти на шальку гирю вагою не більше ніж Р /2. Сила F΄ визначиться як сума ваги гирі і шальки. 5. Відпустити затискач та повільно зменшувати кут нахилу площини (постукуючи молоточком по пластині) доти, доки тіло не почне ковзати (без постукування) від нижнього до верхнього стопора. Записати кут нахилу α1, відпустити площину, зняти гирю з шальки. 6. Обчислити за (3) коефіцієнт тертя k1. 7. Підібрати гирю вагою не більше ніж P/4, покласти її на шальку та, повільно підіймаючи площину і постукуючи молоточком по пластині, знайти кут α2, при якому тіло почне ковзати вниз по пластині. Записати кут нахилу α2, опустити площину і відчепити нитку з шалькою. 8. За формулою (5) знайти k2 і обчислити k за (6). 9. Покласти тіло на пластину, повільно підіймаючи площину і постукуючи молоточком по пластині, знайти кут α3, при якому тіло почне ковзати вниз. За формулою (7) знайти k3 порівняти його зі значенням k, визначивши різницю: Δk = k – k3. 10. Результати вимірювань і розрахунків подати в таблиці:
Дайте відповідь на запитання:
1. Чи велика точність вимірювань коефіцієнта тертя? 2. Що називають кутом тертя? 3. Що таке внутрішнє тертя, зовнішнє тертя?
Лабораторна робота №5. Дослідження основного закону динаміки обертального руху. Прилади та приладдя: хрестоподібний маятник з набором муфт, вертикальний масштаб, набір тягарів 0,10, 0,15, 0,20 кг, штангенциркуль, секундомір. Мета роботи: перевірити здійснення основного закону динаміки обертального руху.
Коротка теорія і метод дослідження
Основний закон динаміки обертального руху твердого тіла навколо нерухомої осі стверджує, що кутове прискорення тіла пропорційне головному моменту зовнішніх сил, що діють на тіло, і обернено пропорційне моменту інерції тіла. β = M / I. (1) де β - кутове прискорення тіла, M - головний момент зовнішніх сил, I - момент інерції тіла відносно осі обертання. Момент інерції тіла є мірою інертності тіла при обертанні і визначається як сума добутків маси кожної частки тіла на квадрат її відстані від осі обертання I = Σ mi ri2 (2) Справедливість закону (1) можна перевірити, вимірюючи кутове прискорення для різних значень моменту сил M та сталого моменту інерції тіла I. В цьому випадку відношення моментів сил Mi до кутових прискорень βi має залишатись сталим: Mi / βi = I = const. (3) В даній роботі вимірюється момент інерції хрестоподібного маятника, що складається з хрестовини та шківа. Момент інерції маятника можна змінювати, закріпляючи на ньому на однакових відстанях R від осі чотири муфти масами m0. Якщо момент інерції хрестоподібного маятника дорівнює I0, то, вважаючи муфти матеріальними точками, загальний момент інерції можна подати у вигляді I = I0 + 4m0R2. (4) Визначення кутового прискорення і моменту сили в умовах даної роботи може бути виконано у такий спосіб. На шків радіусом r намотується нерозтяжна нитка, до якої прикріплено тягар масою m. Під дією сили тяжіння тягар опускається рівноприскорено з прискоренням a, яке пов’язане з кутовим прискоренням співвідношенням: β = a / r. (5) Величину дотичного прискорення a, визначимо із умови спостереження прискореного опускання тягаря масою m. На підвішений на нитці тягар m діє сила натягу нитки F, а вниз - сила тяжіння Землі mg. Рівнодіюча цих сил спрямована вниз і надає тягареві m прискорення a = (mg – F) / m, (6) звідки F = m(g – a). (7) Вантаж проходить відстань h з прискоренням a за проміжок часу t h = at2/2, звiдки a = 2h/t2 (8) Отже, момент сили натягу нитки виявляється рівним M = Fr = m(g – 2h/t2) r (9) Якщо поділити момент сили (9) на кутове прискорення (5) з урахуванням (8), можна одержати момент інерції хрестоподібного маятника. В роботі при трьох різних значеннях вантажу m визначають момент інерції хрестоподібного маятника, а потім – те ж саме, але з додатковими муфтами.
Порядок виконання роботи: Завдання 1.
1. Підвісити на нитку тіло масою 0,10кг. Сумістивши його з верхньою поділкою лінійки, дайте йому можливість опускатись. За допомогою секундоміра виміряйте час опускання. Дослід виконайте тричі. 2. Виміряти радіус шківа, висоту опускання. 3. Для середнього в трьох вимірюваннях часу опускання при сталій висоті обчислити момент інерції хрестоподібного маятника. 4. Повторити дії пп. 1 і 3 для тягарів 0,15 і 0,20 кг. Всі результати подати в таблиці 1.
Таблиця 1. Визначення момента інерції хрестоподібного маятника.
5. Обчислити довірчий інтервал ΔІ0 визначення І0 при надійності 0,7. Кінцевий результат подати у вигляді: І0 = < І0 >. ± ΔІ0. Представити взірець розрахунків для m = 0,1 кг.
Завдання 2.
1. Міцно закріпити 4 муфти на стрижнях маятника на однакових відстанях R від осі обертання. 2. Повторити дії завдання 1. 3. Розрахувати значення моменту інерції I за (4). Результати вимірювань і розрахунків подати в таблицю 2. Таблиця 2.Визначення моменту інерції навантаженого маятника.
Дайте відповідь на запитання:
1. Чи визначається розбіжність результатів вимірювань моменту інерції при різних використовуваних тягарях? 2. В чому причина розбіжності між розрахованим за (4) значенням і виміряним в завданні 2? 3. Чи можна за допомогою подібної лабораторної установки виміряти моменти інерції інших тіл?
Лабораторна робота № 6. Дослідження моментів інерції тіл за допомогою закону збереження енергії. Прилади та приладдя: установка з маховим колесом на осі, шківом для нитки і вертикальним масштабом, штангенциркуль, секундомір, тягар 0,20 кг і набір досліджуваних тіл різних мас та конфігурацій. Мета роботи: засвоїти один із методів вимірювання моментів інерції симетричних тіл.
Коротка теорія і метод вимірювань
Кінетична енергія тіла, що обертається навколо нерухомої осі, може бути представлена як сума кінетичних енергій часток, що складають дане тіло: W = Σ mi vi2 / 2 (1) Виражаючи лінійну швидкість частки через кутову швидкість тіла і радіус кола ri, що описується часткою (vi = ω ri), замість (1) одержимо W = Σ mi ri2 ω2 /2 (2) Величина I = Σ mi ri2 (3) служить мірою інертності тіла при обертальному русі і називається моментом інерції тіла. З урахуванням (3) формула (2) записується у вигляді W = I ω2 / 2 (4) Розрахунки за (3) легко провести у випадку тіл правильної геометричної форми. Моменти інерції тіл складної геометричної форми визначають дослідним шляхом. Один із методів експериментального визначення моментів інерції тіл довільної геометричної форми вивчається в цій лабораторній роботі. Вимірювальна установка складається з маховика з віссю (для зменшення тертя вісь знаходиться в шариковому підшипнику). На осі маховика є шків для намотки нитки з тягарем на кінці. На маховикові для установки і закріплення досліджуваних тіл є також штирі і гвинт для затискування тіл. Нехай тягар знаходиться на висоті h над поверхнею підлоги. Якщо його відпустити, то, опускаючись, він витратить свою потенціальну енергію mgh на виконання роботи проти сил опору F, на надання кінетичної енергії обертовій системі, частина її перейде в кінетичну енергію самого тягаря - mgh = Fh + I ω2 / 2 + m v2 / 2, (5) де Fh - робота по подоланню сил опору: I ω2 / 2 - кінетична енергія обертової системи; mv2/2 - кінетична енергія тягaря, що опускається. Це рівняння покладено в основу вимірювань момента інерції. Вимірювання на установці можуть бути проведені двома методами. Метод 1. Після опускання тягаря його кінетична енергія mv2/2 вважається малою порівняно з іншими складовими (5); обертання маховика продовжується, і за рахунок енергії маховика тягар підіймається на висоту h1. Закон збереження енергії для опускання і підйому в таких умовах записується відповідно у вигляді mgh = Fh + I ω2 / 2; I ω2 / 2= Fh1 + mgh1. (6) З цих рівнянь виключається сила опору F, а кутова швидкість за законами рівноприскореного руху може бути подана виразом ω = 2h/rt, де r - радіус маховика. Для момента інерції системи остаточно одержуємо I = Цей метод можна застосувати, якщо задовольняється умова gt2 / 2h ≥ 1. Метод 2. Може бути застосований без останнього обмеження методу 1. Застосовується рівняння (5). Після опускання тягаря нитка сприсає зі штифта на шківі, котрий продовжує сповільнено обертатися деякий час t1 до повної зупинки. Закон збереження енергії в цьому випадку має вигляд I ω2 / 2= FL, (8) де L = r φ - шлях точок на колі шківа при повороті на кут φ до повної зупинки. З (5) та (8) з урахуванням того, що v = ω r та що при рівноприскореному русі ω = 2h/rt і L = ht1/t, одержуємо розрахункову формулу для момента інерції системи: I = mr2 В обох методах вимірювання проводяться в однаковій послідовності: 1) Визначається момент інерції маховика I0 за формулам: (7) або (9); 2) На маховику закріплюється досліджуване тіло і в такий же спосіб визначається сумарний момент інерції I1; 3) Момент інерції досліджуваного тіла розраховується як різниця I = I1 – I0.
Порядок виконання роботи:
Метод 1.
1. Повертаючи маховик без досліджуваних тіл, намотують нитку на барабан і підіймають тягар на висоту h від підлоги. 2. Надають тягареві можливість опускатись і вимірюють проміжок часу t до удару його об підлогу. 3. Вимірюють висоту h1, на яку підійметься тягар за рахунок енергії обертального руху маховика. Вимірювання роблять тричі і в розрахунках користуються середніми величинам. 4. Вимірюють радіус шківа і за (7) розраховують момент інерції I0. 5. Міцно затискують досліджуване тіло на маховику і повторюють дії пп.1-4, визначаючи сумарний момент інерції I1. 6. Обчислюють момент інерції тіла I = I1 – I0. Результати вимірювань та розрахунків заносять до таблиці 1. Таблиця 1
Метод 2.
1. Тягар на нитці підвішують кільцем за штифт шківа і обертанням маховика підіймають до висоти h від підлоги та вимірюють час його опускання t. 2. Надають тягарю можливості опускатися і вимірюють час опускання t. 3. Утримують секундомір ввімкненим та вимірюють час до повної зупинки маховика t1 і визначають час вільного вибігу маховика як t1 = t΄ - t. 4. За формулою (9) обчислюють момент інерції маховика I0. 5. Міцно закріплюють досліджуване тіло на маховику і повторюють дії по пп.1-4 для тієї ж висоти h та визначають момент інерції маховика з тілом I1. Момент інерції тіла розраховують за формулою I = I1- I0. Результати вимірів та розрахунків подають в таблиці 2. Таблиця 2
Дайте відповідь на запитання:
1. Який з двох методів вимірювань точніший? 2. Які обмеження існують в першому методі? 3. Чи можна застосувати ці методи у випадку несиметричних тіл і чому?
Лабораторна робота № 7. Дослідження непружного удару за допомогою балістичного маятника. Приладдя: установка з маятником і пневморушницею, металічна лінійка з масштабом до 1мм, технічні терези. Мета роботи: засвоїти застосування законів збереження імпульсу і енергії.
Коротка теорія та метод вимірювання
При непружному зіткненні тіла незворотньо деформуються і після зіткнення рухаються як одне ціле. Короткочасне зіткнення тіл - удар - називають центральним, якщо тіла до зіткнення рухаються по прямій, що з’єднує їх центри мас. Такий удар ми розглянемо, тому що після зіткнення тіл, що поступально рухаються, не виникає обертальний рух. Нехай до зіткнення тіло масою m1 рухалося зі швидкістю v1, а тіло з масою m2 - зі швидкістю v2. Після непружного удару тіла m1 і m2 рухаються як одне ціле зі швидкістю u. Згідно з законом збереження імпульсу обчислюється: m1 v1 + m2 v2 = (m1 + m2) u (1) З (1) знаходимо: u = (m1 v1 + m2 v2 ) / (m1 + m2). (2) Закон збереження енергії для цього випадку слід записувати у такому вигляді: m1 v12/2 + m2 v22/ 2 = (m1 + m2) u2 / 2 + A, (3) де А – частина енергії, що витратилась на непружну деформацію тіл і частково перейшла у внутрішню енергію тіл, яку ми будемо називати роботою непружної деформації. Підставляючи u з (2) в (3), отримаєм: A = - найбільш загальне співвідношення для роботи непружної деформації. В основу даної роботи покладено так званий метод балістичного маятника, що представляє собою масивну головку у вигляді циліндра, що підвішений на тонкій спиці. Внутрішня частина головки заповнена пластиліном, спиця з’єднана з маточницею, що містить підшипник. При повороті головки зі спицею навколо осі обертання тим самим забезпечується мінімальне тертя. Перед пострілом з пневматичної рушниці головка знаходиться в стані спокою (v2 = 0). Позначимо швидкість кулі v1 = v. Тоді з (4) випливає: A = W1 де W1 = m1v2/2 - кінетична енергія кулі. Кінетична енергія маятника при відхиленні його в крайне положення повністю переходить в потенціальну енергію (рис.1): (m1 + m2) u2 / 2 = (m1 + m2) g h, (6)
де h - висота підняття головки маятника дорівнює h = R(1 – cosα), де R - відстань від осі обертання до її центру ваги.
Порядок виконання роботи:
1. Відвести маятник вправо із проміжка між щитками, зняти зі спиці головку маятника і визначити її масу m2 на технічних терезах з точністю до 1 г. 2. Надіти головку на спицю, виміряти довжину маятника R і опустити його в положення рівноваги. 3. Зарядити рушницю, зробити постріл і виміряти по середній вертикальній рисці маятника найбільший кут відхилення від положення рівноваги з точністю до 5/ (одна поділка). Зам’яти в пластиліні отвір від кулі. 4. Виконати пп. 2-3 для другої і третьої кулі. 5. Розрахувати швидкість кулі, її кінетичну енергію і роботу деформації A. Маса кулі m2 = 0,286 г. 6. Знайти довірчий інтервал Δv визначення швидкості кулі для надійності 0,7 і подати швидкість кулі у вигляді v = < v > ± v 7. Результати вимірів і розрахунків представити в таблиці.
Результати вимірів і розрахунків швидкості кулі
Дайте відповіді на запитання:
1. Чи можна в розрахунках нехтувати роботою деформації? 4. Що слід зробити, щоб використати установку для більших значень швидкості і маси кулі?
Лабораторна робота № 8. Дослідження пружного удару куль. Приладдя: Установка для вимірювань з двома парами куль і градусною шкалою, лінійка. Мета роботи: засвоїти метод дослідження частково пружного удару.
Коротка теорія і метод вимірювань
При ударі тіл можливі два граничні випадки: кінетична енергія тіл після удару, дорівнює іі ж значенню, до удару (пружний удар) і після удару тіла рухаються як одне ціле (непружний удар). В першому випадку в момент удару відбувається деформація тіла, частина кінетичної енергії тіла переходить в потенціальну енергію пружної деформації. Після удару відбувається повне відновлення форми тіла, потенціальна енергія пружної деформації повністю переходить в кінетичну енергію. В другому випадку не вся початкова кінетична енергія тіл в момент удару переходить в енергію пружної деформації, частина її переходить у внутрішню енергію тіл (внаслідок чого вони нагріваються), і після удару не відбувається відновлення форми тіл. Кінетична енергія після удару виявляється меншою, ніж до удару. Між цими двома граничними випадками удару лежать ча
|

 (3)
(3) = Fb, (5)
= Fb, (5)




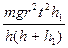 , (7)
, (7) (
(  - 1). (9)
- 1). (9) (v1- v2)2 (4)
(v1- v2)2 (4) , (5)
, (5)





