В прикладных задачах часто нужно определить корреляционную функцию и спектральную плотность по экспериментальным данным. При этом мы можем наблюдать и анализировать только «кусок» реализации на временном интервале от нуля до некоторого  , поэтому для невозможно использовать усреднение по ансамблю. Остается надеяться на то, что процесс эргодический, и применять усреднение по времени.
, поэтому для невозможно использовать усреднение по ансамблю. Остается надеяться на то, что процесс эргодический, и применять усреднение по времени.
Пусть известна реализация случайного процесса 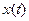 на интервале от 0 до
на интервале от 0 до  . Для оценки (приближенного вычисления) корреляционной функции при
. Для оценки (приближенного вычисления) корреляционной функции при  (то есть при положительных
(то есть при положительных  , достаточно малых по сравнению с
, достаточно малых по сравнению с  ) можно использовать формулу
) можно использовать формулу
 .
. 
(1)
Обратите внимание, что время усреднения равно  , а не
, а не  , потому что только интервал
, потому что только интервал  содержит как
содержит как  , так и
, так и  . К сожалению, точно вычислить этот интеграл невозможно, потому что мы не знаем математическую формулу для
. К сожалению, точно вычислить этот интеграл невозможно, потому что мы не знаем математическую формулу для 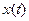 . В реальности обычно известны только значения этой функции (выборка) в моменты
. В реальности обычно известны только значения этой функции (выборка) в моменты  , где
, где  – интервал между измерениями. Тогда
– интервал между измерениями. Тогда  можно приближенно подсчитать только для
можно приближенно подсчитать только для  (где
(где  ) по формуле
) по формуле
 ,
,  , в которой интеграл заменен на сумму.
, в которой интеграл заменен на сумму.
С теоретической точки зрения математическое ожидание такой оценки (при усреднении по ансамблю)совпадает с истинной корреляционной функцией, то есть это – несмещенная оценка.
Оценка спектральной плотности

 , поэтому для невозможно использовать усреднение по ансамблю. Остается надеяться на то, что процесс эргодический, и применять усреднение по времени.
, поэтому для невозможно использовать усреднение по ансамблю. Остается надеяться на то, что процесс эргодический, и применять усреднение по времени.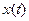 на интервале от 0 до
на интервале от 0 до  (то есть при положительных
(то есть при положительных  , достаточно малых по сравнению с
, достаточно малых по сравнению с  .
. 
 , а не
, а не  содержит как
содержит как  , так и
, так и  . К сожалению, точно вычислить этот интеграл невозможно, потому что мы не знаем математическую формулу для
. К сожалению, точно вычислить этот интеграл невозможно, потому что мы не знаем математическую формулу для  , где
, где  – интервал между измерениями. Тогда
– интервал между измерениями. Тогда  можно приближенно подсчитать только для
можно приближенно подсчитать только для  (где
(где  ) по формуле
) по формуле ,
,  , в которой интеграл заменен на сумму.
, в которой интеграл заменен на сумму.


