Пусть интегральный канал переоборудован по методу обратных разностей
 ,
,
что соответствует разностному уравнению
 . (*)
. (*)
Теперь построим выражение для сигнала  . Учтем, что
. Учтем, что
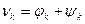 и
и  ,
,
где функция  задает нелинейность типа «насыщение»:
задает нелинейность типа «насыщение»:
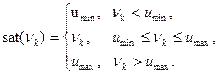
Объединяя эти формулы, получим разностное уравнение для вычисления  :
:
 .
.
В этой формуле значение  , которое требуется рассчитать, входит и в правую часть! Это значит, что для вычисления
, которое требуется рассчитать, входит и в правую часть! Это значит, что для вычисления  требуется не просто подставить в формулу известные значения, а решить нелинейное уравнение относительно
требуется не просто подставить в формулу известные значения, а решить нелинейное уравнение относительно  . Такое явление называется алгебраическим циклом, его желательно избегать. Более того, в сложных случаях это уравнение может не иметь решения вообще. Система Matlab-Simulink выдает предупреждение в случае обнаружения алгебраического цикла (algebraic loop) при моделировании.
. Такое явление называется алгебраическим циклом, его желательно избегать. Более того, в сложных случаях это уравнение может не иметь решения вообще. Система Matlab-Simulink выдает предупреждение в случае обнаружения алгебраического цикла (algebraic loop) при моделировании.
Для того, чтобы не было алгебраического цикла, правая часть разностного уравнения (аналогичного уравнению (*)) не должна зависеть от  . Это будет в том случае, если передаточная функция
. Это будет в том случае, если передаточная функция  – строго правильная, т.е., степень ее числителя меньше степени знаменателя. Из всех рассмотренных вариантов переоборудования интегратора этому условию удовлетворяет метод Эйлера, который мы и будем использовать в работе. При попытке применить метод обратных разностей или преобразование Тастина возникает алгебраический цикл, потому что степени числителя и знаменателя передаточной функции
– строго правильная, т.е., степень ее числителя меньше степени знаменателя. Из всех рассмотренных вариантов переоборудования интегратора этому условию удовлетворяет метод Эйлера, который мы и будем использовать в работе. При попытке применить метод обратных разностей или преобразование Тастина возникает алгебраический цикл, потому что степени числителя и знаменателя передаточной функции  равны.
равны.

 ,
, . (*)
. (*) . Учтем, что
. Учтем, что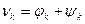 и
и  ,
, задает нелинейность типа «насыщение»:
задает нелинейность типа «насыщение»: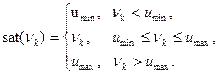
 :
: .
. – строго правильная, т.е., степень ее числителя меньше степени знаменателя. Из всех рассмотренных вариантов переоборудования интегратора этому условию удовлетворяет метод Эйлера, который мы и будем использовать в работе. При попытке применить метод обратных разностей или преобразование Тастина возникает алгебраический цикл, потому что степени числителя и знаменателя передаточной функции
– строго правильная, т.е., степень ее числителя меньше степени знаменателя. Из всех рассмотренных вариантов переоборудования интегратора этому условию удовлетворяет метод Эйлера, который мы и будем использовать в работе. При попытке применить метод обратных разностей или преобразование Тастина возникает алгебраический цикл, потому что степени числителя и знаменателя передаточной функции 


