Лінійна залежність або незалежність систем векторів
1. Підберіть необхідне обладнання. 2.З ’ єднайте фази лампового реостату за схемою «зірка з нейтральним проводом» (рис.3.3, або рис 3.4). 3.Для реалізації симетричного режиму споживача ввімкніть у кожну фазу однакову кількість ламп. Вимірте фазні напруги генератора та споживача, фазні струми, струм у нейтральному проводі. Дані занесіть до табл.8.1. 4. Здійсніть несиметричне навантаження. Для цього ввімкніть в кожній фазі різну кількість ламп. Вимірте фазні напруги генератора та споживача, фазні струми, струм у нейтральному проводі. Дані
Рис. 3.3. Електрична схема з використанням комплекту К-50
Рис. 3.4. Електрична схема з використанням амперметрів
занесіть до таблиці 3.1. 5. Уберіть нейтральний провід. Між клемами z та N ввімкніть вольтметр на 50 В, який буде вимірювати напругу зсуву нейтралі UN. Повторіть виміри. Результати занесіть до таблиці 3.1. 6. Вимірте та запишіть лінійні напруги: UАВ =, UВС =, UСА =.
Таблиця 3.1 Результати експерименту
7. Побудуйте у масштабі векторні діаграми струмів та напруг для кожного режиму. Побудова векторної діаграми
а) "Зірка" з нейтральним проводом (рис. 3.5,а, 3.5,б). Оберіть масштаби зображень для напруг(mU) та струмів (mІ). На комплексній площині відкладіть в масштабі напруг вектори фазних напруг генератора: вектор U А співпадає по фазі з віссю дійсних чисел (+1), вектор U В відстає від нього на кут 1200; вектор U С відстає від U В також на 1200. Оскільки в схемі присутній нейтральний провід, вектори фазних напруг споживача (U a, U b, U с) співпадають з однойменними векторами напруг джерела. Також співпадають нейтральні точки джерела (N) та споживача (n). З'єднаємо між собою кінці векторів U А, U В та U С і отримаємо вектори лінійних напруг U АВ, U ВС, U СА. Оскільки лампи розжарювання представляють собою активний опір, фазні струми співпадають по фазі з однойменними фазними напругами споживача. Відкладіть в масштабі mІ струми I а, I b, I с. Щоб отримати вектор струму в нейтральному проводі I N, згідно з (3.7), треба зробити додавання I а, I b, I с. б) "Зірка" без нейтралі (рис. 3.5,в). Вектори фазних напруг генератора та лінійні напруги відкладаються так само, як і в попередньому випадку. Фазні напруги споживача тепер різні за значенням. Щоб отримати положення точки "n" на векторній діаграмі, спочатку розхилом циркуля, який дорівнює довжині вектора U a, роблять насічку з точки "а"; далі розхилом циркуля, який дорівнює довжині вектора U b, роблять насічку з точки "b". На перетину насічок знаходиться нейтральна точка споживача "n". З'єднайте точку "n" з кінцями векторів U А, U В та U С і отримаєте вектори фазних напруг споживача (U a, U b, U с). Вектор, який проведеній від "N" до "n" буде вектором напруги зсуву фаз U N. Струми фаз відкладаються аналогічно попередньому випадку і співпадають по фазі з однойменними фазними напругами споживача. 8. Користуючись законом Ома, розрахуйте опори фаз Rа, Rb, Rс для несиметричного навантаження. 9. З векторних діаграм визначте величини струму нейтралі та напруги зсуву фаз. Порівняйте їх з експериментальними значеннями.
Рис. 3.5. Приклади векторних діаграм: а) – "зірка" з нейтралью, симетричне навантаження; б) - "зірка" з нейтралью, несиметричне навантаження; в) "зірка" без нейтралі, несиметричне навантаження
Контрольні запитання 1. Як з’єднати фази «зіркою»? 2. Які існують співвідношення між лінійними та фазними напругами та струмами при з’єднанні «зіркою»? 3. Роз’ясніть роль нульового проводу при з’єднанні «зіркою». 4. Що буде, якщо в схемі, яка з'єднана "зіркою" з нейтральним проводом, відбудеться обрив фази? 5. Що буде, якщо в схемі, яка з'єднана "зіркою" без нейтрального проводу, відбудеться обрив фази?
лінійна залежність або незалежність систем векторів 1. Установить линейную зависимость или независимость следующих систем векторов. Система векторов 2. Установить линейную зависимость или независимость следующих систем векторов. Система векторов a1=(2,–9,1), a2=(2,–2,–3), a3=(‑1,‑2,3) трёхмерного пространства. 3. Установить линейную зависимость или независимость следующих систем векторов. Система векторов a1=(1, 1, 1, 0, 0), a2=(1, 0, 1, 0, 1), a3=(1, 0, 0, 1, 0) арифметического пространства 4. Пусть a, b, c – три вектора на плоскости, из которых можно сложить треугольник. Будут ли эти векторы линейно зависимы? 5. Даны два вектора a1=(1, 2, 3, 4), a2=(0, 0, 0, 1). Подобрать ещё два четырёхмерных вектора a3 и a4 так, чтобы система a1, a2, a3, a4 была линейно независимой.
|
, 
, 
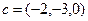трёхмерного пространства.
.
