ОПРЕДЕЛЕНИЕ КРИТИЧЕСКОЙ ТЕМПЕРАТУРЫ САМОВОЗГОРАНИЯ СКОПЛЕНИЯ САМОНАГРЕВАЮЩЕГОСЯ ТВЕРДОГО ДИСПЕРСНОГО МАТЕРИАЛА
Теория теплового самовозгорания (самовоспламенения) позволяет решить прямую и обратную задачу самовозгорания: - по кинетическим параметрам определить критические условия самовозгорания (критические температуры То и Тв); - по критическим условиям определить кинетические параметры (Е и С). Эти задачи можно решать аналитически и графически. Рассмотрим графический способ определения критической температуры самовозгорания ( Известно [3,4], что соотношение между энергией активации (Е) и логарифмом предэкспоненциального множителя (ln С) определяется компенсационным уравнением: Е =
где R - универсальная газовая постоянная, R=8,314 Дж·моль-1·К-1;
Величина
exp
где
Из уравнения (2.1) имеем:
Из выражения (2.3) определяется величина предэкспоненциального множителя С и сравнивается с экспериментальным значением данного материала. Далее проводится расчет адиабатической скорости самонагревания (
При известных значениях С и Е, задаваясь температурами ( Результаты расчета На следующем этапе строится график теплоотвода по уравнению:
где
где
F - поверхность скопления материала,
V - объем скопления,
Коэффициент неравномерности нагрева определяют по формуле:
где
материала до теплофизического центра), м. Затем проводится прямая охлаждения под углом
|

 ) скопления твердого дисперсного материала.
) скопления твердого дисперсного материала. (2.1)
(2.1)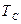 - температура компенсации,
- температура компенсации, 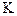 ;
; - адиабатическая скорость самонагревания при температуре Тс,
- адиабатическая скорость самонагревания при температуре Тс, 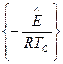 (2.2)
(2.2)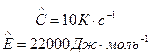 }изокинетические параметры.
}изокинетические параметры. (2.3)
(2.3)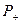 ) для конкретного материала по уравнению Аррениуса:
) для конкретного материала по уравнению Аррениуса: (2.4)
(2.4)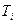 ), находят
), находят 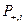 .
. . Для удобства построения графика значения
. Для удобства построения графика значения  , (2.5)
, (2.5)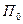 - темп охлаждения. Его вычисляют по формуле:
- темп охлаждения. Его вычисляют по формуле: (2.6)
(2.6) - коэффициент неравномерности нагрева;
- коэффициент неравномерности нагрева;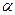 - коэффициент теплоотдачи от поверхности скопления к окружающей среде,
- коэффициент теплоотдачи от поверхности скопления к окружающей среде, 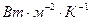 ;
;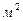 ;
;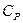 - теплоемкость материала,
- теплоемкость материала,  ;
;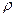 - плотность материала,
- плотность материала,  ;
; .
. (2.7)
(2.7) - относительный градиент
- относительный градиент  ;
;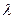 - коэффициент теплопроводности материала,
- коэффициент теплопроводности материала,  ;
; - определяющий размер (расстояние от поверхности
- определяющий размер (расстояние от поверхности и
и  .
.


