КОНТРОЛЬНЫЙ ПРИМЕР
Для того, чтобы построить график адиабатической скорости самонагревания в координатах
Например: Вариант n
Рис. 3.1. Чтобы провести прямые охлаждения, необходимо проделать следующее графические и арифметические действия: - взять - отложить на оси - восстановить из полученных точек перпендикуляры к оси - найти произведения - отложить вертикально вверх на соответствующих перпендикулярных прямых полученные значения Принимаем
Рис 3.2
Находим произведения первая точка: вторая точка: третья точка: четвертая точка: пятая точка: Откладываем вверх по вертикали полученные значения, причем масштаб по вертикальной оси выбрается таким образом, чтобы от последнего полученного значения ( Через две точки строим прямые охлаждения по уравнению
Т, К Рис 3.3
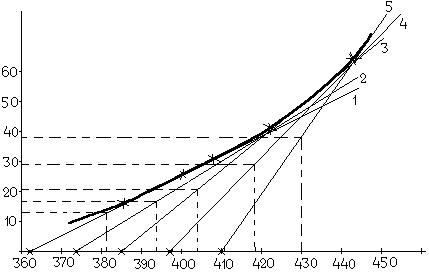
После этого строим кривую температурной зависимости адиабатической скорости самонагревания Кривая адиабатической скорости самонагревания строиться следующим образом. На прямых охлаждения (1, 2, 3, 4 и 5) определяем при помощи лекала возможные точки касания экспоненты и намечаем их координаты. Так для прямой охлаждения 1 экспонента коснется в точке
Рис 3.4 График температурной зависимости адиабатической скорости самонагревания.
Через эти точки проводим по лекалу касательную, получаемую в виде экспоненты, которая описывается зависимостью (3.1). Координаты получаемых точек касания кривой адиабатической скорости самонагревания с прямыми охлаждения заносим в таблицу 3.2.
Таблица 3.2
Путем вычислений заполняем оставшиеся две графы таблицы 3.2 по нижеприведенным соотношениям:
1.
2. Результаты вычислений заносим в последние две графы таблицы 3.3.
Таблица 3.3
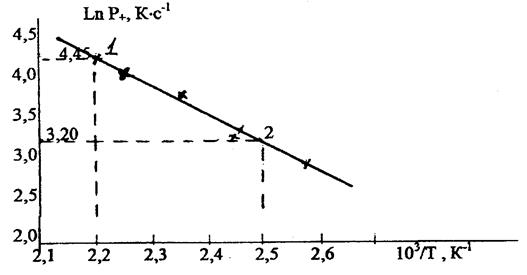
По данным последних двух колонок (табл. 3.3) строим график в координатах Ln(
Рис. 3.5
По полученным на графике (рис. 3.5) точкам строим прямую. Затем на этой прямой выбираем две характерные точки (любые) и координаты этих точек подставляем в следующие соотношения:
1. 2. откуда находим С:
Рис. 3.6 График адиабатической скорости самонагревания в координатах Аррениуса.
|

 ,
,  (как показано на рис. 3.1), необходимо взять из индивидуального задания (таблица 3.1) значения критических температур самонагревания (
(как показано на рис. 3.1), необходимо взять из индивидуального задания (таблица 3.1) значения критических температур самонагревания ( ) и отложить на горизонтальной оси
) и отложить на горизонтальной оси 



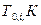
 (произвольно, любое целое число);
(произвольно, любое целое число); значение (
значение ( (полученных значений будет также пять);
(полученных значений будет также пять); .
. ºС и отложим на оси
ºС и отложим на оси  (рис. 3.2).
(рис. 3.2).
 :
: ;
; ;
; ;
;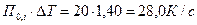 ;
; ;
; ) оставалось ½ тетрадного листа (рис 3.2).
) оставалось ½ тетрадного листа (рис 3.2). на перпендикуляре о381 К. Так получаем прямую охлаждения 1 (см. рис. 3.3). Аналогично строим прямые охлаждения для 2, 3, 4 и 5 прямой.
на перпендикуляре о381 К. Так получаем прямую охлаждения 1 (см. рис. 3.3). Аналогично строим прямые охлаждения для 2, 3, 4 и 5 прямой. К/с
К/с
 . Эта кривая должна проходить таким образом, чтобы она касалась прямых охлаждения только в одной точке и не пересекала этих прямых (рис 3.4);
. Эта кривая должна проходить таким образом, чтобы она касалась прямых охлаждения только в одной точке и не пересекала этих прямых (рис 3.4); ,
,  ; для прямой 2 ―
; для прямой 2 ― 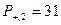 ,
,  ; для прямой 3 ―
; для прямой 3 ―  ,
,  ; для прямой 4 ―
; для прямой 4 ―  ,
,  ; для прямой 5 ―
; для прямой 5 ―  ,
, 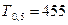 .
. Т,К
Т,К
 , К/с
(из графика)
, К/с
(из графика)
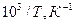 (расчетом)
(расчетом)