ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
МНОГОФАКТОРНОЕ ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТОВ,
Цель занятия: закрепление теоретических знаний, получение практических навыков по планированию экспериментов и обработке экспериментальных данных.
1.1. Теоретический раздел
Описание любой технической системы и получение информации об объекте традиционно начинается с эксперимента. Все методы планирования экспериментов можно разделить на 2 блока [5]: 1. Методы пассивного планирования экспериментов. 2. Методы активного планирования экспериментов. При применении методов пассивного планирования план проведения экспериментов составляют один раз и при выполнении исследований его, как правило, не меняют. Наиболее ярким представителем этого блока является метод последовательного изменения переменных. При применении методов активного планирования, эксперименты ставятся небольшими сериями, результаты каждой серии обрабатываются и анализируются. При необходимости создаётся план следующей серии, по результатам обработки которой вырабатывается дальнейшая стратегия. К рассматриваемым методам относятся: полный факторный эксперимент, дробный факторный эксперимент, метод латинских квадратов, симплекс-решетчатое планирование и ряд других. При применении методов полного и дробного факторных экспериментов изменяются одновременно не один, а несколько факторов. На первом этапе математическая модель процесса представляется в виде линейной зависимости вида
где a0, a1,…,an – коэффициенты модели, которые определяются по экспериментальным данным; x1,…xn – входные переменные. При применении степенных зависимостей вида
Рисунок 1.1 - Графическое представление плана полного факторного эксперимента
При математической обработке экспериментальные значения выходных переменных и входных переменных также предварительно логарифмируются. При применении полного и дробного факторных экспериментов можно учитывать также взаимодействия входных переменных, уравнение (1.1) дополняется членами вида Например, при исследовании влияния режима резания на стойкость режущего инструмента Т, (рисунок 1.1), будем одновременно изменять скорость резания V и подачу S, опыты проводим при значениях переменных, определяемых точками 1, 2, 3, 4 плана. Для унификации процедуры планирования и обработки экспериментальных данных введем новую систему координат X1, X2 с началом в центре плана (S= 0,6мм/об, V= 2м/ с). Выберем маштаб новых переменных так, чтобы при минимальных значениях V и S (нижний уровень варьирования) переменные X1, X2 были равны -1, а при максимальных значениях V и S (верхний уровень варьирования) - +1. Расчет координат точек в новой системе выполняется по зависимости
где S0 – значение переменной на основном уровне S = (Smax+ Smin) /2 = 0,6; έS – интервал варьирования переменной (для S равен έS = (Smax - Smin) /2 = 0,4). Рассмотрим последовательность обработки экспериментальных данных при многофакторном планировании на примере исследования скорости резания и подачи на стойкость инструмента. Данные экспериментальных исследований сведены в таблицу 1.1. Таблица 1.1. Результаты экспериментальных исследований
При составлении матрицы, табл. 1.1, столбик X1 X2, определяющий взаимодействие переменных, получен их произведением. С целью возможности определения дисперсии и оценки воспроизводимости в каждой точке плана выполнено по два опыта. Математическая модель процесса представляется линейным полиномом, который для рассматриваемого примера имеет вид
Обработка экспериментальных данных выполняется в следующей последовательности: 1. Оценка воспроизводимости процесса. При одинаковом числе параллельных опытов при каждом сочетании уровней факторов воспроизводимость процесса (отсутствие значительных отклонений) определяют по критерию Корена. Сравнивается максимальная величина дисперсии с суммарной. Критерий вычисляется по формуле:
где N – число параллельных опытов. Если расчетный критерий оказывается меньше табличного или равен ему, то процесс считается воспроизводимым. Для выполненных экспериментов G = 0,72/1,56 = 0,46; Gтабл = 0,9065, следовательно, процесс является воспроизводимым. 2. Если процесс воспроизводим, то определяют дисперсию воспроизводимости или ошибку опыта:
Для примера 3. Вычисление коэффициентов регрессии полинома
где Xij - значение i -й переменной в j -й строке;
Для примера а0 = 240,0/4 = 80; а1 = ((-1)67,5+(+1)56,5+(-1)62,5+(+1)53,5)/4 = -5; а2 = -2; а3 = 0,5. Зависимость для расчета выходной переменной с учетом полученных значений коэффициентов примет вид
4. Выполним оценку значимости коэффициентов регрессии с помощью критерия Стьюдента. Коэффициент считается значимым, если выполняется неравенство
где В уравнении (1.6) незначим коэффициент а3 = 0,5. С учетом этого уравнение перепишется
4. Оценка адекватности линейной модели выполняется по критерию Фишера, для чего определяется дисперсия адекватности
где k – число коэффициентов линейной модели не считая а0. Для примера Критерий Фишера по дисперсии адекватности вычисляется по уравнению
Для примера F = 1/0,39 = 2,6. Табличное значение критерия равно 7,7. Следовательно, полученная линейная модель адекватна реальному процессу. При получении адекватной модели она записывается в явном виде подстановкой входных переменных из уравнения (1.2) в уравнение (1.1).
1.2. Порядок выполнения расчетов
1) составить матрицу планирования и выполнить обработку экспериментальных данных при исследовании влияния режима резания на стойкость режущего инструмента и шероховатость поверхности. 2) составить матрицу планирования и выполнить обработку экспериментальных данных при исследовании влияния пробега автомобиля от начала эксплуатации, массы перевозимого груза и скорости на расход топлива. Данные для расчетов выдаются преподавателем.
1.3. Содержание отчета
1. Краткие сведения из теории многофакторного планирования экспериментов. 2. Данные задания на выполнение работы. 3. Математическая обработка экспериментальных данных. 4. Выводы по работе.
1.4. Контрольные вопросы
1. Какие методы планирования экспериментов используются при моделировании поведения системы? 2. С какой целью применяют методы многофакторного планирования экспериментов? 3. Чем отличаются полный и дробный факторные эксперименты? 4. С какой целью проводится анализ воспроизводимости экспериментальных данных? 5. С какой целью проводится проверка адекватности математической модели?
|

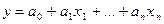 , (1.1)
, (1.1) они приводятся к виду (1.1) логарифмированием.
они приводятся к виду (1.1) логарифмированием.


 . Для удобства вычислений план эксперимента преобразовывают. Переносят начала координат и меняют масштаб переменных.
. Для удобства вычислений план эксперимента преобразовывают. Переносят начала координат и меняют масштаб переменных. , (1.2)
, (1.2)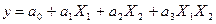 . (1.3)
. (1.3)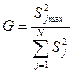 , (1.4)
, (1.4)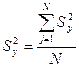 . (1.5)
. (1.5)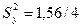 = 0,39.
= 0,39. ;
; 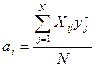 , (1.6)
, (1.6) - среднее значение выходной переменной в j -й строке.
- среднее значение выходной переменной в j -й строке. . (1.7)
. (1.7) , (1.8)
, (1.8) определяется по таблицам, для примера
определяется по таблицам, для примера  = 2,77 и
= 2,77 и  .
. . (1.9)
. (1.9)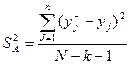 , (1.10)
, (1.10) .
. . (1.11)
. (1.11)


