ОПТИМИЗАЦИЯ МАРШРУТА ОБРАБОТКИ (ПЕРЕВОЗКИ ГРУЗА) МЕТОДОМ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
Цель занятия: закрепление теоретического материала, приобретение навыков решения задач оптимального управления техническими системами.
2.1. Теоретический раздел
Системный подход позволяет не только исследовать поведение и структуру системы, но и определить наиболее рациональные условия ее эксплуатации. Рассмотрим систему, имеющую вектора входных X, выходных Y(t) переменных, управляющих U(t) и возмущающих Ω(t) воздействий. Из векторов входных и выходных переменных выделим параметры объекта (состояние заготовки, состояние перевозимого груза). Отметим особенности изменения параметров состояния объекта: а) за период обработки параметры состояния объекта изменяются от начального Y(0) до конечного Y(N). Начальное и конечное состояния, как правило, не могут изменяться произвольно; б) изменение параметров может происходить либо непрерывно, либо дискретно; в текущий момент времени параметры объекта (фазовые координаты), как правило, отличаются от начальных и конечных; в) скорость изменения параметров существенно зависит от входных переменных и законов изменения управляющих воздействий. Закон изменения фазовых координат объекта для дискретной системы может быть записан в виде уравнений
Для каждой точки фазового пространства имеется допустимая область управления U(t), причем
Для выбора оптимальной траектории имеется критерий эффективности, который зависит от текущих значений фазовых координат и принятого управления каждого этапа
где Общая задача оптимального управления может быть сформулирована следующим образом: зная начальное и конечное состояния объекта (2.1) найти такое допустимое управление (2.2), которое придает функционалу (2.3) максимальное (минимальное) значение. Для непрерывных процессов зависимости (2.1)-(2.3) принимают вид
Для процесса, который не имеет управляющего воздействия, ставится задача определения оптимальных значений входных переменных. Зависимости математической модели будут иметь вид
Для таких процессов необходимо при известных начальных и конечных значениях фазовых координат объекта найти такие допустимые значения входных переменных, которые придают критерию эффективности максимальное (минимальное) значение. Наиболее распространенным методом решения задач оптимального управления дискретными системами является метод динамического программирования. Для выбора оптимальных значений входных переменных применяют метод линейного программирования, метод геометрического программирования и другие. Граф возможных комбинаций маршрута технологического процесса обработки заготовки (перевозки груза) представлен на рисунке 2.1. Квадратами обозначены состояния объекта (промежуточные пункты), стрелками – операции (дороги). При выполнении работы над каждой стрелкой необходимо проставить себестоимость выполнения операции (стоимость перевозки груза). Оптимальный маршрут определяется по рекуррентному соотношению
где
Рисунок 2.1 - Возможные маршруты перевозки грузов
2.2. Порядок выполнения расчетов
Рассчитать оптимальный маршрут перевозки груза из пункта А в пункт В, обеспечивающий наименьшую себестоимость, методом динамического программирования.
2.3. Индивидуальное задание
Каждый студент выполняет индивидуальное задание, выбрав вариант по таблице 2.1. Таблица 2.1 - Варианты заданий для расчета оптимального маршрута
2.4. Содержание отчета
1) Краткие сведения из теории оптимального управления и методе динамического программирования. 2) Граф маршрута обработки детали (перевозки груза) с указанием стоимости отдельных этапов. 3) Расчет оптимального маршрута. 4) Выводы по работе.
2.5. Контрольные вопросы
1) Сформулируйте задачу оптимального управления. 2) Что принимается за критерий оптимизации в технических системах? 3) В чем заключается сущность динамического программирования? 4) Что такое рекуррентное соотношение? 5) Какие задачи решаются методом динамического программирования?
|

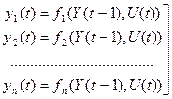 . (2.1)
. (2.1) . (2.2)
. (2.2) , (2.3)
, (2.3) - значение критерия эффективности первого этапа, определяемого по состоянию объекта предшествующего этапа и принятому управлению.
- значение критерия эффективности первого этапа, определяемого по состоянию объекта предшествующего этапа и принятому управлению.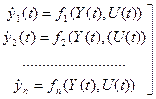 ; (2.4)
; (2.4) ; (2.5)
; (2.5) . (2.6)
. (2.6)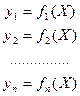
 ; (2.7)
; (2.7)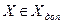 ; (2.8)
; (2.8)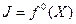 . (2.9)
. (2.9)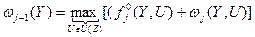 , j = 1, 2, …, N, (2.10)
, j = 1, 2, …, N, (2.10) и
и 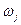 - максимальные значения критерия эффективности заключительной части процесса соответственно начиная с j-1 -го и j –го этапов;
- максимальные значения критерия эффективности заключительной части процесса соответственно начиная с j-1 -го и j –го этапов;  - значение критерия эффективности j-1 – го этапа.
- значение критерия эффективности j-1 – го этапа.



