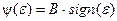Задача № 1
Определить условия устойчивости нелинейной САУ, используя критерий абсолютной устойчивости В.М. Попова.
Передаточная функция линейности части системы для всех вариантов имеет следующий вид:
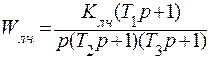 .
.
Структурная схема системы имеет вид, представленный на рис. 17.
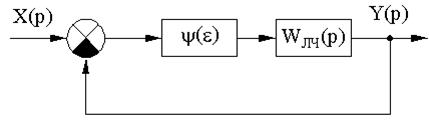
Рис. 17
Вид и параметры нелинейных элементов и линейной части системы для различных вариантов заданы в таблице 2.
| Таблица 2
|
| Вариант
| Вид нелинейности
| В
| а
| Клч
| Т1
| Т2
| Т3
|
|
|
усилитель с ограничением
|
|
|
| 0.5 с
| 1 с
| 1 с
|
|
|
|
| 2.5
| 0.5 с
| 2.5 с
| 5 с
|
|
|
|
|
| 0.1 с
| 0.5 с
| 10 с
|
|
|
| 0.5
|
| 0.1 с
| 1 с
| 2.5 с
|
|
|
| 0.25
|
| 0.01с
| 0.5 с
| 1 с
|
|
|
| 0.3
|
| 0.02с
| 0.1 с
| 0.5 с
|
| Продолжение таблицы 2
|
|
|
трехпозиционное реле
|
| 0.5
|
| 0.2 с
| 2 с
| 8 с
|
|
|
|
|
| 0.5 с
| 2 с
| 5 с
|
|
|
| 0.5
|
| 1 с
| 6.5 с
| 2 с
|
|
|
| 0.25
|
| 0.01 с
| 0.5 с
| 1 с
|
|
|
| 0.3
| 4.5
| 0.05 с
| 0.1 с
| 0.8 с
|
|
|
| 0.4
|
| 0.25 с
| 0.5 с
| 1 с
|
| Вариант
| Вид нелинейности
| В
| a1
| a2
| Клч
| Т1
| Т2
| Т3
|
|
|
усилитель с зоной
нечувствительности
и ограничением
|
| 0.2
| 0.6
| 2.5
| 0.5 с
| 1 с
| 1 с
|
|
|
| 0.4
|
| 3.0
| 1.5 с
| 10 с
| 5 с
|
|
|
| 0.5
|
| 2.0
| 2 с
| 10 с
| 20 с
|
|
|
| 0.2
| 0.8
| 5.0
| 1 с
| 12 с
| 8.2 с
|
|
|
| 0.1
| 0.4
| 4.5
| 0.1 с
| 0.8 с
| 1.5 с
|
|
|
| 0.2
| 0.8
|
| 0.5 с
| 2 с
| 4 с
|
|
|
| 0.4
| 0.8
|
| 1 с
| 5 с
| 10 с
|
| Окончание таблицы 2
|
| Вариант
| Вид нелинейности
| В
| a
| Клч
| Т1
| Т2
| Т3
|
|
|
двухпозиционное реле
с гистерезисом
|
| 0.2
|
| 0.1
| 0.5
|
|
|
|
| 0.4
|
| 0.08
| 0.5
| 1.5
|
|
|
| 0.6
| 2.5
| 0.5
| 0.75
| 1.25
|
|
|
| 0.8
|
| 0.75
|
|
|
|
|
| 0.6
|
| 0.5
|
| 2.5
|
|
|
| 0.4
|
| 0.8
| 1.25
| 2.5
|
| Вариант
| Вид нелинейности
| В
| a1
| a2
| Клч
| Т1
| Т2
| Т3
|
|
|
 Трехпозиционное реле с гистерезисом
Трехпозиционное реле с гистерезисом
|
| 0.2
| 0.4
|
| 0.05
| 0.1
| 0.8
|
|
|
| 0.3
| 0.6
| 4.5
| 0.5
|
|
|
|
|
| 0.4
| 0.8
|
| 0.75
| 0.25
|
|
|
|
| 0.25
| 0.8
|
| 0.5
| 0.25
|
|
|
|
| 0.2
| 0.6
|
|
| 2.5
| 0.5
|
Задача № 2
Построить фазовый портрет нелинейной системы, заданной следующей структурной схемой (рис. 18). Линейная часть системы для всех вариантов одинакова.
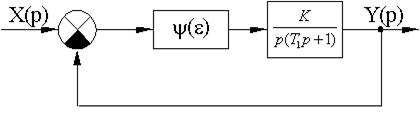
Рис. 18
Вид и параметры нелинейных элементов и линейной части системы для различных вариантов заданы в таблице 3.
| Таблица 3
|
| Вариант
| Вид нелинейности
| В
| а
| К
| Т1
|
|
|
усилитель с ограничением
|
| 0.5
|
| 0.1 с
|
|
|
|
|
| 1 с
|
|
|
| 1.5
|
| 1 с
|
|
|
|
| 12.5
| 0.5 с
|
|
|
| 0.8
|
| 0.75 с
|
|
|
| 0.5
| 8.5
| 1.25 с
|
|
|
| 0.75
|
| 2.5 с
|
|
|
| 0.6
| 4.5
| 0.8 с
|
Продолжение таблицы 3
| Вариант
| Вид нелинейности
| В
| а
| К
| Т1
|
|
|
трехпозиционное реле
|
| 0.5
|
| 1 с
|
|
|
|
|
| 0.5 с
|
|
|
| 0.5
|
| 1 с
|
|
|
| 0.2
| 4.5
| 0.5 с
|
|
|
| 0.4
|
| 0.25 с
|
|
|
| 0.6
| 2.5
| 0.75 с
|
|
|
| 0.8
|
| 0.8 с
|
|
|
|
| 12.5
| 1.5 с
|
|
|
двухпозиционное реле
с гистерезисом
|
| 0.5
|
| 1 с
|
|
|
|
|
| 2 с
|
|
|
|
|
| 0.5 с
|
|
|
| 0.8
|
| 1 с
|
|
|
| 0.4
| 12.5
| 0.5 с
|
|
| 1.5
| 0.6
| 7.5
| 0.75 с
|
|
|
| 0.8
|
| 0.8 с
|
|
|
|
|
| 1 с
|
|
| 1.5
| 0.5
|
| 1.5 с
|
Окончание таблицы 3
| Вариант
| Вид нелинейности
| В
| К
| Т1
|
|
| 
двухпозиционное реле
|
|
| 0.5 с
|
|
| 1.5
| 8.5
| 1 с
|
|
|
| 4.5
| 1.25 с
|
|
|
|
| 1.5 с
|
|
|
|
| 2 с
|
Задача № 3
Исследовать динамику нелинейной системы методом гармонического баланса. Структурная схема системы имеет следующий вид (рис.19):

Рис. 19
Вид и параметры нелинейных элементов и линейной части системы для различных вариантов заданы в таблице 4.
| Таблица 4
|
| Вариант
| Вид НЭ
| Уравнение НЭ
| В
| а
| Клч
| Т1
| Т2
| Т3
|
|
|
усилитель с
ограничением
| 
|
| 0.5
|
| 2 с
| 0.5 с
| 5 с
|
|
|
|
|
| 1 с
| 0.2 с
| 2.5 с
|
|
|
| 0.6
|
| 2.5 с
| 0.4 с
| 3 с
|
|
|
| 0.25
|
| 0.5 с
| 1.5 с
| 2.5 с
|
|
|
| 0.4
|
| 0.1 с
| 0.5 с
| 2.5 с
|
|
|
| 0.8
| 12.5
| 0.75 с
| 1 с
| 2.5 с
|
|
|
|
|
| 1 с
| 5 с
| 7.5 с
|
|
|
| 1.5
|
| 0.4 с
| 1 с
| 0.8 с
|
Продолжение таблицы 4
| Вариант
| Вид НЭ
| Уравнение НЭ
| В
| а
| Клч
| Т1
| Т2
| Т3
|
|
|
двухпозиционное
реле
с гистерезисом
| 
|
|
|
| 1 с
| 0.5 с
| 2.5 с
|
|
|
| 0.5
|
| 2.5 с
| 0.5 с
| 10 с
|
|
|
| 0.4
|
| 0.5 с
| 1 с
| 0.07 с
|
|
|
| 0.25
|
| 0.5 с
| 4.5 с
| 0.8 с
|
|
|
| 0.4
|
| 1 с
| 0.9 с
| 1.8 с
|
|
|
| 0.6
|
| 0.75 с
| 2.5 с
| 5 с
|
|
|
| 0.8
|
| 1.5 с
| 12.5 с
| 5 с
|
|
|
| 0.5
|
| 2.5 с
| 1 с
| 5 с
|
|
|
трехпозиционное
реле
| 
|
| 0.5
|
| 0.5 с
| 1 с
| 5 с
|
|
|
|
|
| 0.05 с
| 0.5 с
| 1 с
|
|
|
|
|
| 0.08 с
| 0.5 с
| 0.01 с
|
|
|
| 0.5
|
| 0.5 с
| 1 с
| 0.1 с
|
|
|
| 0.4
| 12.5
| 0.2 с
| 0.8 с
| 1.5 с
|
|
| 1.5
| 0.8
|
| 0.4 с
| 1.5 с
| 2.5 с
|
|
|
|
|
| 0.8 с
| 5 с
| 7.5 с
|
|
|
| 1.2
|
| 0.5 с
| 2.5 с
| 0.05 с
|
|
|
| 0.6
|
| 0.5 с
| 0.75 с
| 0.05 с
|
Окончание таблицы 4
| Вариант
| Вид НЭ
| Уравнение НЭ
| В
| Клч
| Т1
| Т2
| Т3
|
|
|  двухпозиционное реле двухпозиционное реле
| 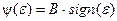
|
|
| 0.5 с
| 0.1 с
| 1.5 с
|
|
|
| 7.5
| 0.25 с
| 0.5 с
| 2.5 с
|
|
|
|
| 0.75 с
| 2.5 с
| 12.5 с
|
|
|
|
| 0.05 с
| 0.5 с
| 0.75 с
|
|
|
|
| 0.01 с
| 0.5 с
| 1.25 с
|
Задача № 4
Исследовать устойчивость и построить график переходного процесса в импульсной системе с АИМ, заданной следующей структурной схемой
(рис. 20):
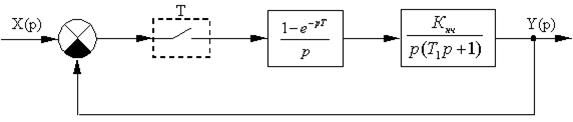
Рис. 20
Параметры непрерывной части и период квантования (Т) заданы в таблице 5:
| Таблица 5
|
| Вариант
| Т
| Кнч
| Т1
| Вариант
| Т
| Кнч
| Т1
|
|
| 0.01 с
| 10 1/c
| 1 c
|
| 0.1 с
| 10 1/c
| 10 c
|
|
| 0.5 с
| 15 1/c
| 2 c
|
| 0.5 с
| 5 1/c
| 5 c
|
|
| 0.05 с
| 15 1/c
| 0.5 c
|
| 0.1 с
| 20 1/c
| 0.5 c
|
|
| 0.01 с
| 20 1/c
| 0.5 c
|
| 1 с
| 5 1/c
| 0.5 c
|
|
| 0.05 с
| 5 1/c
| 1 c
|
| 0.5 с
| 10 1/c
| 1 c
|
|
| 0.005 с
| 10 1/c
| 1 c
|
| 0.05 с
| 10 1/c
| 10 c
|
|
| 0.25 с
| 15 1/c
| 2 c
|
| 0.25 с
| 5 1/c
| 5 c
|
|
| 0.025 с
| 15 1/c
| 0.5 c
|
| 0.05 с
| 20 1/c
| 0.5 c
|
|
| 0.005 с
| 20 1/c
| 0.5 c
|
| 0.5 с
| 5 1/c
| 0.5 c
|
|
| 0.025 с
| 5 1/c
| 1 c
|
| 0.25 с
| 10 1/c
| 1 c
|
|
| 0.005 с
| 10 1/c
| 0.5 c
|
| 0.05 с
| 10 1/c
| 5 c
|
|
| 0.25 с
| 15 1/c
| 1 c
|
| 0.25 с
| 5 1/c
| 2.5 c
|
|
| 0.025 с
| 15 1/c
| 0.25 c
|
| 0.05 с
| 20 1/c
| 0.25 c
|
|
| 0.005 с
| 20 1/c
| 0.25 c
|
| 0.5 с
| 5 1/c
| 0.25 c
|
|
| 0.025 с
| 5 1/c
| 0.5 c
|
| 0.25 с
| 10 1/c
| 0.5 c
|

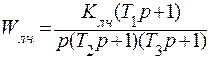 .
.
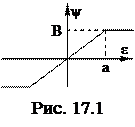



 Трехпозиционное реле с гистерезисом
Трехпозиционное реле с гистерезисом











 двухпозиционное реле
двухпозиционное реле