Задача №2. Расчет устойчивости систем.
Расчет устойчивости систем. Рассчитать устойчивость системы, заданной следующей структурной схемой (рис 22.) и построить кривую D-разбиения по коэффициенту усиления САУ в разомкнутом состоянии.
Рис. 22
W1(P)=k1; W2(P)= Параметры звеньев: k1=12; k2=80; k3=0.15; k4=2; T2=0.5; T3=10; T4=2.
1. Критерий Гурвица.
Запишем эквивалентную передаточную функцию системы Wзам(р) = Запишем передаточную функцию системы, разомкнутой по главной обратной связи. Wраз(p) = W1(P) ×W2(P) ×W3(P) ×W4(P) = Характеристическое уравнение системы. D(p)=1+ Wраз(p)=0 ® D(p)=1+
Kэ+(Т2Т3р3+Т2р2+Т4р+р)(Т32р2+2Т3р+1)=0; Kэ=К1К2К3К4;
Kэ + Т2Т4Т32 р5 + (2Т2Т4Т3 + Т2Т32 + Т4Т32) р4 + (Т4Т2 + 2Т2Т3 + 2Т4Т3 + Т32) р3 +
Подставляя численные значения, получаем:
Т.к. все коэффициенты положительны, то первое условие Гурвица выполняется. Составим матрицу из коэффициентов характеристического уравнения и вычислим определители:
D1=270>0; D2=270•151-100•22,5=38520>0
Т.к. D4 меньше нуля то система неустойчива.
2. Критерий Рауса.
Коэффициенты первого столбца таблицы должны быть положительны.
100р5+270р4+151 р3+ 22,5р4+ р+288=0
Т.к. с15<0, то система неустойчива.
3. Критерий Михайлова.
Уравнение характеристического вектора получим из характеристического уравнения заменой оператора р®jw. D(p)= 100р5+270р4+151 р3+ 22,5р2+ р+288=0; D(jw)=100(jw)5+270 (jw)4+151(jw)3+22,5(jw)2+jw+288 = 100jw5+270jw4-151jw3- -22,5jw2+jw+288 = (288-22.5w2+270w4)+jw(1-151w2+100w4)=Re(w)+Im(w). Изменяя w в интервале 0<w<¥, рассчитываем Re(w) и Im(w) и заносим в таблицу 1. Таблица 1
Т.к. годограф начинается на положительном отрезке вещественной оси (рис. 23.), но не обходит 5 квадрантов, то система неустойчива. Рис. 23
4. Критерий Найквиста.
Определяем устойчивость по АФЧХ системы, разомкнутой по главной обратной связи. Wраз(p)= W1(P)* W2(P)* W3(P) * W4(P)= Комплексный коэффициент передачи САУ получим, заменяя p®jw Wраз(jw)= Выведем действительную и мнимую части домножая числитель и знаменатель на комплексно-сопряженные множители.
Re= Задаваясь значениями w из промежутка 0 £ w < ¥, рассчитываем Re(w) и Im(w).
Таблица 2
По данным таблицы строим АФЧХ системы (рис. 24).
Система неустойчива т.к. при дополнении годографа дугой с бесконечным радиусом до положительного отрезка вещественной оси АФЧХ охватывает критическую точку с координатами (–1; 0j). Определим устойчивость, используя ЛАЧХ и ФЧХ системы.
Уравнение для построения ЛАЧХ системы:
20 lg|W(jw)| = 20 lgКэ – 20 lgw – 10 lg(1+T22w2) – 20 lg(1+T32w2) – 10 lg(1+T42w2)
20 lg Kэ = 20 lg 288 = 49,19
Асимптотическую ЛАЧХ легко построить по ЛАЧХ типовых звеньев, суммируя их. Для этого рассчитывают частоты излома
Уравнение для построения ФЧХ системы j(w) = – 90 – arctg(wT2) – 2 arctg(wT3) – arctg(wT4) =
САУ будет устойчива в замкнутом состоянии, если ЛАЧХ пересекает ось частот раньше, чем ФЧХ пересекает линию -180° (рис. 25.). Значит система неустойчива.
5. Метод D-разбиений по коэффициенту усиления.
100р5+270р4+151р3+22,5р2+р+288 = 0, Ксис= 288.
Выражаем коэффициент усиления системы из характеристического уравнения системы: Ксис= -100р5-270р4-151 р3- 22,5р2- р. Заменим p®jw
Ксис= -100(jw)5-270 (jw)4-151(jw)3-22,5(jw)2-jw =
По этому выражению, изменяя 0<w<¥, строим кривую, которая затем дополняется зеркальным отображением относительно оси Х,и заштриховываем (рис. 26.) в соответствии с правилами.
Рис. 26
Претендентом на область устойчивости является область 1. Определим корни характеристического уравнения (определим устойчивость) при К, взятом из этой области, по критерию Гурвица.
100 р5 + 270 р4 +151 р3 + 22,5 р2 + р + К=0
К=0.1 – получим все отрицательные корни.
Таким образом, САУ будет устойчива, если 0<K<0,14.
Критический коэффициент усиления системы можно определить, используя любой из критериев. D-разбиение позволяет выделить области с различным расположением корней характеристического уравнения на комплексной плоскости при изменении какого-либо параметра (в нашем случае К).
Задача №3 Выбрать структуру и параметры последовательного КУ.
Пусть система имеет следующую передаточную функцию в разомкнутом состоянии:
и параметры: К=60, Т1=1 с, Т2 = 0.5 с, Т3 = 0.1 с.
Построим ЛАЧХ и ФЧХ системы, для этого рассчитаем частоты излома:
Уравнение ФЧХ системы
j(w) = - 90 – arctg wT1 – arctg wT2 – arctg wT3
Построим ЛАЧХ и ФЧХ системы (рис. 27).
Рис. 27 Система с астатизмом первого порядка, поэтому ЛАЧХ в области низких частот, до первой сопрягающей частоты имеет наклон -20 дБ/дек. Продолжение этого наклона до оси частот дает частоту равную добротности системы по скорости, т.е. равную коэффициенту усиления. На частоте w=1 ордината ЛАЧХ равна 20lg(K), т.е. 20lg(K)=35,56 дБ. Проведем вертикальные линии, соответствующие частотам излома. После первой сопрягающей частоты наклон ЛАЧХ увеличивается на -20дБ/дек, т.е. становится равным -40 дБ/дек. Аналогично увеличиваются наклоны после каждой последующей частоты излома. По построенной ЛАЧХ определяем частоту среза – пересечение ЛАЧХ с осью частот, wср»5 1/с. j(w) = – 90 – arctg 5×1 – arctg 5×0,5 – arctg 5×0,1 > - 180, система неустойчива. Для выбора структуры и параметров КУ последовательного типа построим ЛАЧХ скорректированной системы. По заданию коэффициент усиления должен быть меньше в 2 раза, как и частота среза; wср ск=2,5 1/с, Кск=Dск=30. Следовательно, на частоте w=1 ордината скорректированной системы равна: 20lg(30) = 29,56» 30 дБ. Через wср ск=2,5 проводим ЛАЧХ с наклоном -20дБ/дек. и через ординату на w=1, равную 30 дБ также линию с наклоном -20 дБ/дек. Сопряжение этих двух участков выполняем наклоном -40 дБ/дек – в областях низких частот и высоких частот. Протяженность участка с наклоном -20 дБ/дек на частоте среза должна быть не меньше одной декады, чтобы обеспечить запасы устойчивости. Рекомендуется выбирать соседние частоты сопряжения для скорректированной ЛАЧХ на расстоянии не менее одной трети декады. ЛАЧХ скорректированной системы желательно сформировать так, чтобы как можно больше частот сопряжения исходной и скорректированной систем совпадали. Частоты излома для ЛАЧХ скорректированной системы определяем графически и записываем соответствующую ей передаточную функцию и уравнение для j(w). w1’=0.8 (1/с) T1’=1,25 c; w2’=w1=1 T2’=1 c; w3’=w3=10 T3’=0.1 c; w4’=30 T4’=0.03 c;
j(w) = – 90 – arctg 1,25×w + arctg w – arctg 0,1×w - 2 arctg 0,03 w; j(wср) = – 90 – arctg 2,5×1,25× + arctg 2,5 – arctg 0,25 - 2 arctg 0,075 =-116,7.
Строим j(w) и проверяем запас по фазе (Δj=180 - j(wср)). Если запас по фазе не удовлетворяет условию, увеличиваем протяженность участка с наклоном -20 дБ/дек на частоте среза. Передаточная функция КУ
По ЛАЧХ Lку(w) определяется простым вычитанием ординат Lск(w) – Lисх(w) = Lку(w). По виду Lку(w) подбираем корректирующие четырехполюсники и рассчитываем их параметры (R, C). Наше КУ можно представить тремя участками, изображенными на рис. 28.
Рис. 28
Подбираем для них соответствующую электрическую схему (справочные таблицы КУ).
Выбираем С (из условий габаритов) и рассчитываем R1 и R2 . С=50 мкФ. Рис. 29
Для L2:
Рис. 30
Аналогично выбираем С и рассчитываем R1 и R2, для этой и последующей цепочки. Для L3 выбираем такую же цепочку, как и для L2, но другими будут параметры:
Соединяя последовательно эти цепи, получим коэффициент преобразования их, равный
Таким образом, общая электрическая схема КУ:
Рис. 31 Задача №4
Для скорректированной системы (в задаче №3) рассчитать и построить переходную характеристику h(t) и определить показатели качества.
Переходная характеристика системы – это реакция ее на единичное ступенчатое воздействие. Уравнение переходной характеристики можно получить, решая дифференциальное уравнение, используя теоремы разложения Хевисайда и изображение переходной функции. Теоремы Хевисайда гласят следующее. 1. Если изображение Лапласа некоторой функции представляет собой отношение полиномов и является правильной дробью, то оригинал этой функции определяется выражением
где
2. Если изображение Лапласа некоторой функции можно представить как
Если найдены корни характеристического уравнения, уравнение h(t) легко определяется. Можно промоделировать систему или использовать стандартное матобеспечение для решения дифференциального уравнения n-го порядка. По переходной характеристике определяют tр – время регулирования, h% - перерегулирование. Точность системы можно оценить, используя теорему о пределах и вычислив h(¥).
tр – время от начала переходного процесса до момента,
Рис. 32
2B=5% ×h(:)
|


 ;W3(P)=
;W3(P)=  ; W4(P)=
; W4(P)= 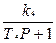 .
. .
. .
. .
. .
.

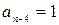












 .
. .
. ;
; ;
; .
.
 .
.



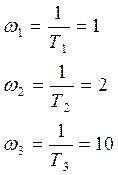


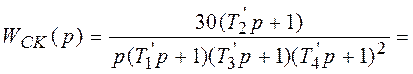


 ,
,
 Для L1:
Для L1: (из справочника)
(из справочника) ;
; 
 ;
; 

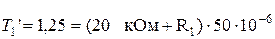



 ;
; 
 ;
; 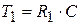
 ;
; 
 с
с 
 . Наше КУ должно иметь коэффициент преобразования равный 0,5, следовательно, надо поставить согласующие усилители с общим коэффициентом усиления:
. Наше КУ должно иметь коэффициент преобразования равный 0,5, следовательно, надо поставить согласующие усилители с общим коэффициентом усиления: .
.
 ,
, - изображение переходной функции,
- изображение переходной функции, , pi – корни характеристического уравнения системы.
, pi – корни характеристического уравнения системы.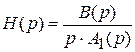 , то оригинал ее определится следующим выражением:
, то оригинал ее определится следующим выражением:




 .
.


