Теоретический материал.
Задания для контрольной работы 15.1 – 15.10. Случайная величина Х задана функцией распределения F(x). Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины Х. 15.1. 15.2. 15.3. 15.4. 15.5. 15.6. 15.7. 15.8. 15.9. 15.10.
Варианты контрольной работы 1. Даны два вектора 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25) 2. Доказать, что векторы 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25) 3. Определить при каком значении параметра k векторы 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25) 4. Даны вершины тетраэдра ABCD. Найти высоту опущенную из вершины D. Определить угол, образуемый ребром AD с плоскостью основания. 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25) 5. Даны координаты вершин треугольника ABC. Составить уравнения сторон треугольника, уравнение медианы и высоты, проведенных из вершины A. Найти длину высоты, опущенной из вершины B. Сделать чертёж в плоскости xOy. 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25) 6. Определить тип кривых второго порядка и их основные параметры. Сделать чертёж. 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25) 7. Найти угол между плоскостями. Написать каноническое уравнение линии пересечения плоскостей. 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25) 8. Найти точку M пересечения прямой l и плоскости π. Написать уравнение прямой, проходящей через точку A: а) параллельно данной прямой (l1); б) перпендикулярно данной плоскости (l2 ). Найти точку B, симметричную данной точке A относительно данной плоскости. 1) l: 2) l: 3) l: 4) l: 5) l: 6) l: 7) l: 8) l: 9) l: 10) l: 11) l: 12) l: 13) l: 14) l: 15) l: 16) l: 17) l: 18) l: 19) l: 20) l: 21) l: 22) l: 23) l: 24) l: 25) l: Теоретический материал. Векторы. Основные операции над векторами Вектор – направленный отрезок. Вектор характеризуется длиной и направлением. Длина вектора – расстояние между началом и концом отрезка. Начало вектора не фиксируется, его можно приложить к любой точке пространства. Два вектора равны, если они одной длины и одинаково направлены. Два вектора называются коллинеарными, если они лежат на параллельных прямых. Коллинеарные векторы делятся на сонаправленные и противоположно направленные: Векторы называются компланарными, если они лежат на параллельных плоскостях или в одной плоскости. На трех некомпланарных векторах, как на составляющих, можно построить параллелепипед.
3. Умножение на число:
1) Теорема 1: Два ненулевых вектора Теорема 2: В плоскости любой вектор Теорема 3: Три вектора компланарны, когда один из них можно записать в виде линейной комбинации двух других. Теорема 4: В пространстве R3 существует единственное разложение вектора Проекция вектора на ось и координаты вектора
Скалярная проекция на ось – это число, равное по абсолютной величине длине вектора Т.е. Можно доказать, что скалярная проекция 1) 2) Пусть даны некомпланарные векторы:
Координаты т. М определяют как координаты её радиус-вектора. Действия с векторами в координатной форме Если Длина этого вектора равна Если Пусть Из последней формулы имеем, что если два вектора коллинеарны, то их координаты пропорциональны, т.е. Пусть вектор
Вектор Векторы Очевидно, что
Скалярное произведение векторов, основные свойства Скалярным произведением двух векторов Свойства: 1. 2. 3. 4. Доказательство: 5. 6. Физический смысл скалярного произведения это работа по перемещению материальной точки по вектору 7. Если Векторное произведение векторов Три вектора Векторным произведением двух векторов Свойства векторного произведения: 1. 2. 3. Если Следствие: 4. 5. Если 6. Геометрический смысл векторного произведения: модуль векторного произведения равен площади параллелограмма, построенного на этих векторах как на составляющих. 7. Физический смысл векторного произведения: векторное произведение угловой скорости на радиус–вектор движущийся по окружности точки равно линейной скорости этой точки. Смешанное произведение векторов Смешанным произведением трех векторов Свойства смешанного произведения: 1. Если 2. Геометрический смысл смешанного произведения: модуль смешанного произведения равен объёму параллелепипеда, построенного на этих векторах как на составляющих. 3. Три ненулевых вектора компланарны тогда и только тогда когда их смешанное произведение равно нулю. Различные уравнения прямой в плоскости Прямая – это линия первого порядка, т.е. переменные x и y входят в уравнение линейно (в первой степени).
a(x–x1)+b(y–y1)=0 – уравнение прямой, проходящей через данную точку, перпендикулярную данному вектору. Если в последнем уравнении раскроем скобки, то получим общее уравнение прямой: ax+by+c=0 .
Уравнение прямой, проходящей через т. А(x1; y1) с заданным угловым коэффициентом имеет вид: y–y1=k(x–x1) (6). Уравнение прямой, отсекающей на оси ОХ отрезок b с угловым коэффициентом k, запишется y=kx+b (7). Если прямая l задана уравнением ax+by+c=0, то расстояние от точки М(x0; y0) до l можно найти по формуле: Взаимное расположение прямых. Если l1: a1x+b1y+c1=0, а l2: a2x+b2y+c2=0 и если а если
|







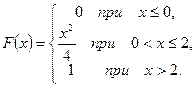



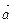 и
и 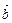 . Найти угол между ними и площадь треугольника построенного на этих векторах как на составляющих. Определить высоту треугольника, опущенную на сторону
. Найти угол между ними и площадь треугольника построенного на этих векторах как на составляющих. Определить высоту треугольника, опущенную на сторону 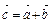 и
и 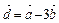 ?
?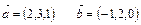


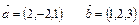











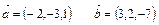









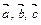 некомпланарны. Найти разложение
некомпланарны. Найти разложение  по векторам
по векторам  .
.



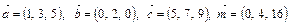



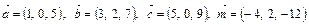












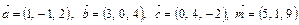



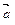 и
и  ортогональны.
ортогональны.



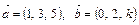

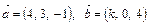


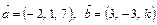





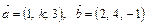




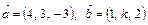

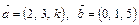





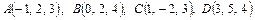




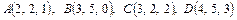

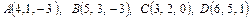
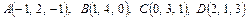



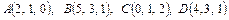


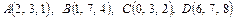








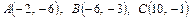







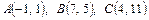













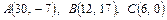
 ;
;  ;
;  ;
;  .
. ;
; 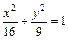 ;
; 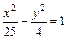 ;
;  .
.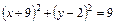 ;
;  ;
;  ;
;  .
. ;
;  ;
;  ;
;  .
.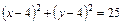 ;
;  ;
;  .
.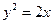 .
. ;
;  ;
;  ;
;  .
. ;
;  ;
;  ;
;  .
. ;
; 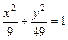 ;
;  ;
;  ;
; 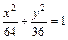 ;
;  ;
; 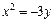 .
. ;
;  ;
; 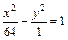 ;
;  .
.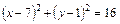 ;
;  ;
;  .
. ;
;  ;
;  .
. ;
;  ;
;  .
. ;
; 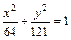 ;
;  ;
;  .
. ;
;  ;
;  ;
;  .
. ;
;  ;
; 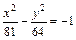 ;
; 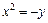 .
.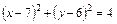 ;
;  ;
;  ;
;  ;
; 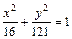 ;
;  ;
;  .
. ;
;  ;
;  .
. ;
;  ;
;  ;
;  ;
;  ;
;  ;
; 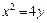 .
. ;
;  ;
; 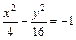 ;
;  ;
;  .
.




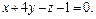
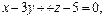




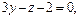


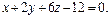

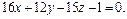





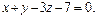










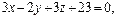










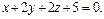


 ; π:
; π:  ; A(2, 1, 1).
; A(2, 1, 1). ; π:
; π:  ; A(4, -1, 0).
; A(4, -1, 0). ; π:
; π:  ; A(1, 2, -1).
; A(1, 2, -1). ; π:
; π:  ; π:
; π:  ; A(7, 4, 1).
; A(7, 4, 1). ; π:
; π:  ; A(2, -4, 1).
; A(2, -4, 1). ; π:
; π:  ; A(0, 5, 7).
; A(0, 5, 7).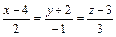 ; π:
; π:  ; A(1, -1, 5).
; A(1, -1, 5). ; π:
; π:  ; A(2, 0, -1).
; A(2, 0, -1). ; π:
; π: 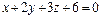 ; A(-1, -1, 2).
; A(-1, -1, 2). ; π:
; π:  ; A(1, 1, 1).
; A(1, 1, 1). ; π:
; π:  ; A(9, 7, 0).
; A(9, 7, 0). ; π:
; π:  ; A(0, 5, 8).
; A(0, 5, 8). π:
π:  A(0, 2, 0).
A(0, 2, 0). π:
π: 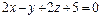 A(1, 2, 0).
A(1, 2, 0). π:
π:  A(1, 7, 6).
A(1, 7, 6). π:
π:  π:
π:  A(1, 2, 1).
A(1, 2, 1). π:
π: 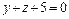 A(1, 2, -4).
A(1, 2, -4). π:
π: 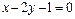 A(1, 1, 1).
A(1, 1, 1). π:
π:  A(1, -1, 7).
A(1, -1, 7). π:
π: 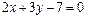 A(0, 8, 3).
A(0, 8, 3). π:
π:  A(2, 2, 0).
A(2, 2, 0). π:
π: 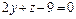 A(1, -1, 2).
A(1, -1, 2). π:
π:  A(1, 2, -3).
A(1, 2, -3). – сонаправленные,
– сонаправленные,  - противоположно направленные.
- противоположно направленные.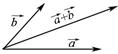
 Действие с векторами: 1. Сложение:
Действие с векторами: 1. Сложение: 2. Вычитание:
2. Вычитание: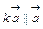 . Если k >0, то
. Если k >0, то  ;
; если k <0, то
если k <0, то  . Справедливы следующие свойства:
. Справедливы следующие свойства: ; 2)
; 2)  .
. и
и 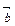 компланарны тогда и только тогда, когда существует число
компланарны тогда и только тогда, когда существует число  такое, что
такое, что  .
. можно разложить по двум данным некомпланарным векторам
можно разложить по двум данным некомпланарным векторам  .
. по трем некомпланарным векторам
по трем некомпланарным векторам 
 Пусть в пространстве даны две точки А и В, через них проведем плоскости a и b, перпендикулярные оси l, которые пересекают ось в точках А1 и В1. Тогда вектор
Пусть в пространстве даны две точки А и В, через них проведем плоскости a и b, перпендикулярные оси l, которые пересекают ось в точках А1 и В1. Тогда вектор 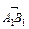 – это проекция вектора
– это проекция вектора  на ось l.
на ось l.
 , где
, где  .
. (
( )=
)=  где
где  .
. . Числа x, y, z – это координаты разложения вектора
. Числа x, y, z – это координаты разложения вектора  ,
,  соответственно. Если базисные векторы взаимно перпендикулярны и имеют единичную длину, то они определяют прямоугольно-декартовую систему координат в пространстве.
соответственно. Если базисные векторы взаимно перпендикулярны и имеют единичную длину, то они определяют прямоугольно-декартовую систему координат в пространстве.

 - радиус-вектор т. М
- радиус-вектор т. М
 , то
, то  .
. .
. , то
, то  .
. , тогда
, тогда  , а
, а  .
. .
.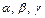 , тогда
, тогда  где
где  направляющие косинусы вектора
направляющие косинусы вектора 
 орт вектора
орт вектора  сонаправлены и
сонаправлены и  .
. , откуда имеем
, откуда имеем  ,
,  ,
,  .
. называется число, равное произведению модулей этих векторов на косинус угла между ними:
называется число, равное произведению модулей этих векторов на косинус угла между ними: 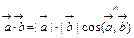 .
.


 .
. , где
, где 
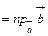 .
. ;
; 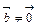 (
(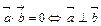 )
) под действием силы
под действием силы  :
: 
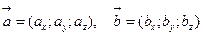 , то
, то 
 кратчайшее перемещение от
кратчайшее перемещение от  называется вектор
называется вектор  перпендикулярный данным, образующий с ними правую тройку, а его длина равна произведению длин данных векторов, умноженному на синус угла между данными векторами:
перпендикулярный данным, образующий с ними правую тройку, а его длина равна произведению длин данных векторов, умноженному на синус угла между данными векторами: 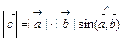 .
.

 ;
;  , то
, то 


 , то
, то 


 , то
, то  Основные уравнения прямой.
Основные уравнения прямой.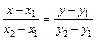 – это уравнение прямой, проходящей через две данные точки А(х1, у1) и В(х2, у2)..
– это уравнение прямой, проходящей через две данные точки А(х1, у1) и В(х2, у2).. .
. Пусть прямая l проходит через т. А (х1, у1), перпендикулярную
Пусть прямая l проходит через т. А (х1, у1), перпендикулярную  :
: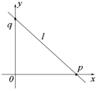 Пусть прямая l отсекает на координатных осях отрезки p и q. A(p; 0); B(0; q) точки пересечения с осями, тогда
Пусть прямая l отсекает на координатных осях отрезки p и q. A(p; 0); B(0; q) точки пересечения с осями, тогда  это уравнение прямой в отрезках.
это уравнение прямой в отрезках.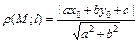 .
.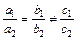 , то l1 || l2,
, то l1 || l2, , то l1 º l2 , если a1a2+b1b2=0, то l1 ^ l2.
, то l1 º l2 , если a1a2+b1b2=0, то l1 ^ l2.


