Примеры решения задач. Задача 1. Даны два вектора и
Задача 1. Даны два вектора Из определения скалярного произведения следует что Вычислим: Тогда Из свойств векторного произведения следует Вычислим векторное произведение С другой стороны Вычислим Два вектора коллинеарны, если их координаты пропорциональны. В данном случае это условие не выполнено, так как Задача 2. Доказать, что векторы Если векторы компланарны, то их смешанное произведение равно нулю. Вычислим смешанное произведение векторов.
Разложение вектора
Следовательно Задача 3. Определить при каком значении параметра k векторы Если векторы ортогональны, то их скалярное произведение равно нулю.
Задача 4. Даны вершины тетраэдра A Найдём координаты векторов:
Определим площадь основания тетраэдра Высоту определим из формулы Вектор Задача 5. Даны координаты вершин треугольника A(1, 2), B(-3, -1), C(4, -2). Составить уравнения сторон треугольника, уравнение медианы и высоты, проведенных из вершины A. Найти длину высоты, опущенной из вершины B. Сделать чертёж в плоскости xOy. Составим уравнение сторон треугольника по формуле прямой проходящей через две данные точки AB: АС: ВС: Высота
Медиана АМ проходит через середину отрезка ВС точку М М Длина высоты равна расстоянию от точки В до прямой АС. Это расстояние найдём по формуле Задача 6. Определить тип кривых второго порядка и их основные параметры. Сделать чертёж. 1) 2) Эксцентриситет эллипса: Директриса: 3) Эксцентриситет эллипса: Директриса: Асимптоты гиперболы: 4) Задача 7. Найти угол между плоскостями Угол между плоскостями равен углу между их векторами нормали Тогда Вектор нормали искомой прямой это векторное произведение
Найдем точку принадлежащую прямой. Для этого решим систему: Задача 8. Найти точку M пересечения прямой l: Запишем параметрическое уравнение прямой l: Решим систему Если прямые параллельны, то их направляющие векторы коллинеарны, то есть уравнение прямой l1: Направляющий вектор прямой, перпендикулярной плоскости будет вектор нормали данной плоскости. Тогда l2: Точка B лежит на прямой l2. Середина отрезка AB – это точка О пересечения прямой и плоскости. Найдём её координаты.
ОСНОВНАЯ ЛИТЕРАТУРА: 1. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. М., Наука, 1986. – 576 С. 2. Луканкин Г.Л., Мартынов Н.Н., Шадрин Г.А., Яковлев Г.Н. Высшая математика: пособие для студентов пединститутов. – М.: Просвещение, 1988. – 431 с. 3. Баврин И.И. Курс высшей математики. Учебник для студентов пединститутов. - М., Просвещение,1992. – 400 с. 4. Пак В.В., Носенко Ю.Л. Высшая математика. – Донецк: Сталкер, 1997. – 599 с. 5. Шипачёв В.С. Курс высшей математики. Учебник. – М.: Проспект, 2004. – 600 с. ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА 1. Письменный Д.Т. Конспект лекций по высшей математике: полный курс. – М.: Айрис – Пресс, 2006. – 608 с. 2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах (в двух частях). М., Высшая школа, 1980. – Ч.1. – 320 с., Ч.2. – 365 с.
|

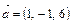 и
и 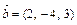 . Найти угол между ними и площадь треугольника построенного на этих векторах как на составляющих. Определить высоту треугольника, опущенную на сторону
. Найти угол между ними и площадь треугольника построенного на этих векторах как на составляющих. Определить высоту треугольника, опущенную на сторону  . Будут ли коллинеарны векторы
. Будут ли коллинеарны векторы 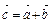 и
и 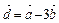 ?
?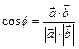 .
.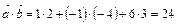 ;
; 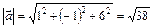 ;
;  .
.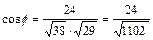 . Следовательно
. Следовательно 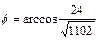 .
.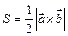 .
. . Тогда
. Тогда 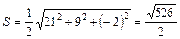 .
. . Откуда следует
. Откуда следует 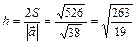 .
.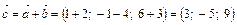 и
и 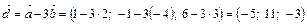 .
. .
.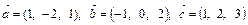 некомпланарны. Найти разложение
некомпланарны. Найти разложение 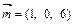 по векторам
по векторам 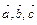 .
.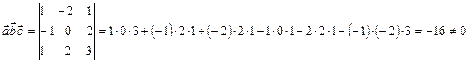 , значит векторы компланарны.
, значит векторы компланарны.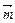 по векторам
по векторам 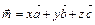 . В координатной форме этому уравнению соответствует система
. В координатной форме этому уравнению соответствует система  Решим эту систему по правилу Крамера.
Решим эту систему по правилу Крамера. 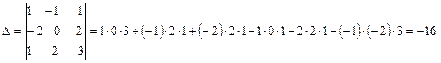 ;
; 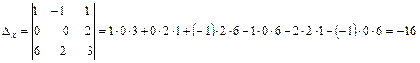 ;
; 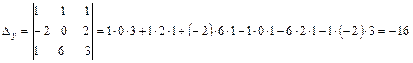 ;
; 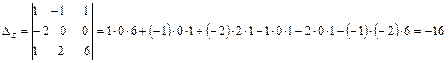 .
.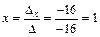 ;
; 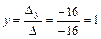 ;
; 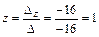 .
.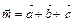
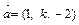 и
и 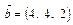 ортогональны.
ортогональны.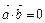 ;
;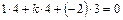 ;
;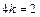 ;
;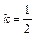 .
.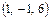 , B
, B 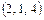 , C
, C 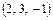 , D
, D 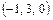 . Найти высоту опущенную из вершины D. Определить угол, образуемый ребром AD с плоскостью основания.
. Найти высоту опущенную из вершины D. Определить угол, образуемый ребром AD с плоскостью основания.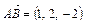 ;
;  ;
; 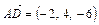 . Вычислим объём тетраэдра по формуле
. Вычислим объём тетраэдра по формуле 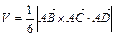 .
.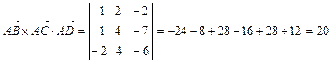 . Тогда
. Тогда  .
.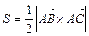
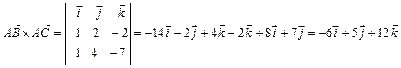 .
. 
 :
: 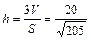 .
.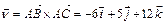 является вектором нормали плоскости основания тетраэдра. Из определения скалярного произведения и формул приведения следует, что
является вектором нормали плоскости основания тетраэдра. Из определения скалярного произведения и формул приведения следует, что 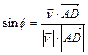 .
. 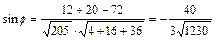 . Откуда находим
. Откуда находим 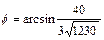 .
.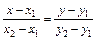 .
.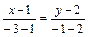
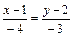

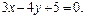


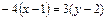
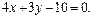
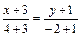
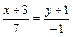
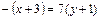
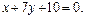
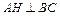 , то есть вектор нормали основания
, то есть вектор нормали основания 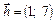 является направляющим вектором высоты. Используя каноническое уравнение прямой
является направляющим вектором высоты. Используя каноническое уравнение прямой 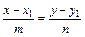 , получим
, получим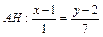
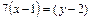

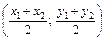 .
.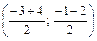 или М(0,5; -1,5). Тогда уравнение медианы АМ:
или М(0,5; -1,5). Тогда уравнение медианы АМ: 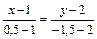
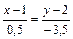
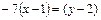

 :
: 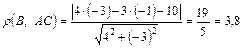 .
.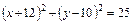 -- окружность с центром в точке
-- окружность с центром в точке  и радиусом равным пяти.
и радиусом равным пяти.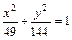 -- эллипс с центром в точке
-- эллипс с центром в точке  , большой полуосью b=12, малой полуосью a=7, расстояние от центра до фокуса
, большой полуосью b=12, малой полуосью a=7, расстояние от центра до фокуса 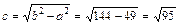 .
.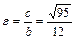 .
. .
.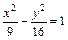 - гипербола с центром в точке
- гипербола с центром в точке 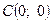 , мнимой полуосью b=4, действительной полуосью a=3, расстояние от центра до фокуса
, мнимой полуосью b=4, действительной полуосью a=3, расстояние от центра до фокуса  .
.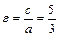 .
.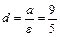 .
.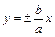

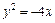 - парабола с вершиной в точке
- парабола с вершиной в точке 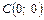 и расстоянием от фокуса до директрисы 2. Ветви направлены в лево.
и расстоянием от фокуса до директрисы 2. Ветви направлены в лево.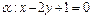 и
и  . Написать каноническое уравнение линии пересечения плоскостей.
. Написать каноническое уравнение линии пересечения плоскостей.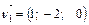 и
и 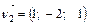 . Тогда
. Тогда 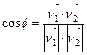 .
.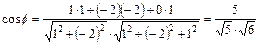 . Следовательно
. Следовательно 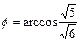 .
. .
.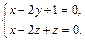 Одну координату зададим сами, например
Одну координату зададим сами, например  . Тогда
. Тогда 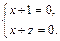 Очевидно, что эта точка
Очевидно, что эта точка 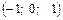 . Уравнение прямой найдем по формуле
. Уравнение прямой найдем по формуле 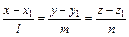 :
: 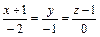 .
.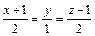 и плоскости π;:
и плоскости π;: 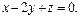 Написать уравнение прямой, проходящей через точку A(1; -2; -1): а) параллельно данной прямой (l1); б) перпендикулярно данной плоскости (l2 ). Найти точку B, симметричную данной точке A относительно данной плоскости.
Написать уравнение прямой, проходящей через точку A(1; -2; -1): а) параллельно данной прямой (l1); б) перпендикулярно данной плоскости (l2 ). Найти точку B, симметричную данной точке A относительно данной плоскости.
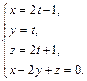 Для этого подставим значения x, y, z из первых трех уравнений в четвертое, получим
Для этого подставим значения x, y, z из первых трех уравнений в четвертое, получим 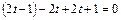 . Откуда
. Откуда 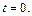 Подставляя в систему найдём M(-1; 0; 1).
Подставляя в систему найдём M(-1; 0; 1).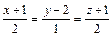
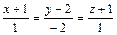 .
.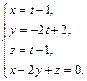 Для этого подставим значения x, y, z из первых трех уравнений в четвертое, получим
Для этого подставим значения x, y, z из первых трех уравнений в четвертое, получим 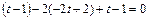 . Откуда
. Откуда 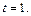 Подставляя в систему найдём О(0; 0; 0). С другой стороны координаты точки О, как середины отрезка
Подставляя в систему найдём О(0; 0; 0). С другой стороны координаты точки О, как середины отрезка 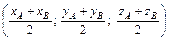 . Приравняв соответствующие координаты и подставив в полученные формулы координаты точки А, получим В(-1; 2; 1).
. Приравняв соответствующие координаты и подставив в полученные формулы координаты точки А, получим В(-1; 2; 1).


