Приложения определенного интеграла
4.1. Площадь плоской криволинейной трапеции.
Пример 13. Вычислить площадь фигуры, ограниченной линиями:
Решение. Построим фигуру, площадь которой надо вычислить. Одной из линий является параболой с вершиной в точке С с координатами (3;4). Вторая линия - прямая.
Для этого решаем систему уравнений Фигура ACB не является криволинейной трапецией, поэтому для вычисления площади данной фигуры рассмотрим разность площадей двух криволинейных трапеций: FACB и FAB. Для вычисления площадей воспользуемся формулой:
Для фигуры FAB
Площадь искомой фигуры будет равна:
Решение. Построим данную кривую. Полярные координаты точек кривой получаются заданием значений угла Вычислим площадь данной фигуры по формуле: Подставляя все эти величины в формулу, получаем:
4.2. Вычисление длины дуги кривой. Пример 15. Вычислить длину дуги кривой: Решение. Данная кривая задана в параметрическом виде, то есть x и y зависят от параметра t. Поэтому, чтобы построить точку с координатами (x,y) нужно задать некоторое значение параметра и потом посчитать x и y. Построим график и найдем точки пересечения с осями координат:
Длина дуги вычисляется по формуле Для данной задачи Подставляя все эти значения в формулу, получаем:
|

 .
.
 , ее решением являются точки A(2;3), B(5;0).
, ее решением являются точки A(2;3), B(5;0). , где a и b это пределы, в которых изменяется переменная х. В данном случае для обеих фигур a=2, b=5. Из чертежа видно, что для фигуры FACB
, где a и b это пределы, в которых изменяется переменная х. В данном случае для обеих фигур a=2, b=5. Из чертежа видно, что для фигуры FACB  . Вычислим площадь этой фигуры:
. Вычислим площадь этой фигуры:

 , следовательно, имеем:
, следовательно, имеем: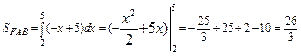 .
. .
.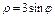 .
. и вычислением значений
и вычислением значений  из равенства
из равенства  . Положение точки А
. Положение точки А  на плоскости в полярной системе координат определяют расстоянием
на плоскости в полярной системе координат определяют расстоянием  , образованным отрезком ОА с полярной осью.
, образованным отрезком ОА с полярной осью. , где
, где  и
и  пределы, в которых лежит данная фигура. В нашем случае
пределы, в которых лежит данная фигура. В нашем случае  .
. .
. , между точками пересечения с осями координат.
, между точками пересечения с осями координат.
 .
. .
.



