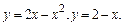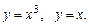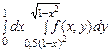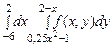Изменение порядка интегрирования в двойном интеграле
Пример 16. Изменить порядок интегрирования в двойном интеграле Решение. Вычисление этого интеграла производится повторным интегрированием: сначала вычисляется интеграл
Для изменения порядка интегрирования необходимо сначала начертить область интегрирования D, которая ограничена линиями х =1, х =3, y=-x, y= -x. Уравнения линий берутся в соответствии с пределами интегрирования. На рисунке область D – это трапеция ABFK. Координаты точек A,B,F,K находим, решая соответствующие системы уравнений. Таким образом получили A(1;1), B(3;3), F(3,-3), K(1;-1). При изменении порядка интегрирования первое интегрирование теперь проводится по переменной y, а второе -–по переменной x. В этом случае при задании области D переменная y изменяется от –3 до 3, а переменная x от линии FKAB до линии FB. Если прямая FB задается одним уравнением х =3, то ломаная FKAB – тремя: х =1, y=-x, y= -x. Таким образом, область интегрирования D имеет смысл представить как объединение трех областей, каждая из которых задается своей системой неравенств: FKE: KACE: ACB: Нашли, что исходный двойной интеграл после замены порядка интегрирования записывается в виде суммы трех двойных интегралов:
Задание № 1. Найти неопределенные интегралы (результаты в случаях а), б) проверить дифференцированием)
Задание № 2. Вычислить с помощью замены переменной определенный интеграл.
Задание № 3. Вычислить несобственный интеграл или доказать его расходимость.
Задание № 4. Вычислить площадь фигуры, ограниченной линиями с указанными ниже уравнениями. Сделать чертеж.
Задание 5.
1. Вычислить длину дуги кривой, заданной уравнением 2. Вычислить объем тела образованного вращением вокруг оси ОУ фигуры, ограниченной линиями 3. Вычислить длину дуги кривой 4. Вычислить объем тела, образованного вращением вокруг оси ОУ фигуры, ограниченной линиями 5. Вычислить объем тела, образованного вращением вокруг оси ОУ фигуры, ограниченной линиями 6. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями 7. Вычислить длину дуги кривой 8. Вычислить объем тела, образованного вращением вокруг оси ОУ фигуры, ограниченной линиями 9. Найти длину кардиоиды 10. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями 11. Вычислить длину дуги кривой 12. Вычислить объем тела, образованного вращением вокруг оси ОХ 13. Вычислить длину дуги кривой 14. Вычислить длину дуги кривой 15. Вычислить объем тела, образованного вращением вокруг оси ОУ фигуры, ограниченной линиями 16. Вычислить длину дуги кривой 17. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной графиками функций 18. Вычислить длину дуги кривой 19. Вычислить длину дуги кривой 20. Найти длину дуги циклоиды 21. Вычислить длину дуги кривой 22. Вычислить длину дуги параболы 23. Вычислить длину дуги кривой 24. Вычислить длину дуги кривой 25. Вычислить длину дуги кривой 26. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной графиками функций 27. Вычислить длину дуги кривой 28. Вычислить длину дуги кривой 29. Вычислить длину дуги кривой 30. Вычислить длину дуги кривой 31. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями 32. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями 33. Вычислить длину дуги кривой 34. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями 35. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями 36. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями 37. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями 38. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями 39. Вычислить объем тела, образованного вращением вокруг оси ОУ фигуры, ограниченной линиями 40. Вычислить длину дуги кривой, заданной уравнениями
Задание 6. Изменить порядок интегрирования в двойных интегралах:
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа для втузов.-М.: Наука, 1973. –720 с.. 2. Пискунов Н.С. Дифференциальное и интегральное исчисление. -М.: Наука, 1972. - Т.1 -456 с. 3. Письменный Д. Конспект лекций по высшей математике. 1 часть. М.: Айрис-пресс, 2007.- с.193-257. 4. Попов А.Г.,Данко П.Е., Кожевникова Т.Я.. Высшая математика в упражнениях и задачах. ч.1,2. – М.: Высшая школа, 1999г.
|

 .
. , а затем поолучившаяся функция интегрируется по переменной х на отрезке [1;3].
, а затем поолучившаяся функция интегрируется по переменной х на отрезке [1;3].


 .
. +
+  +
+ 
 ЗАДАНИЯ КОНТРОЛЬНОЙ РАБОТЫ
ЗАДАНИЯ КОНТРОЛЬНОЙ РАБОТЫ




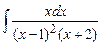
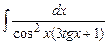






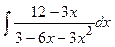








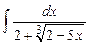

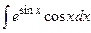


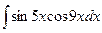
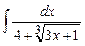






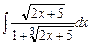

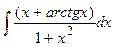





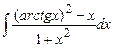




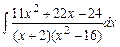
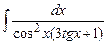




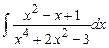


















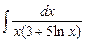






















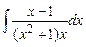









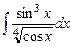

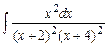





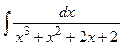

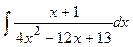








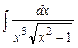
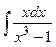










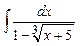




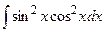



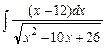

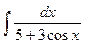







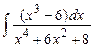

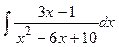


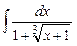


































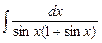














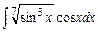




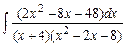

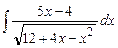

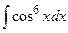






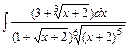








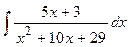











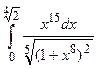


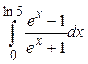
















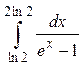



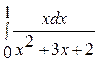











 .
.

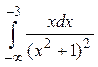






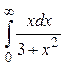




















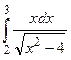













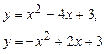



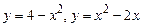








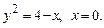

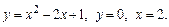


 , от x= -1 до х=1.
, от x= -1 до х=1.
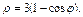

 от точки А(0,0) до точки В(4,8).
от точки А(0,0) до точки В(4,8).
 , лежащей между ее точками пересечения с осью ОХ.
, лежащей между ее точками пересечения с осью ОХ. ,
, 

 .
.

 .
. , отсекаемой прямой х=1.
, отсекаемой прямой х=1.
 от х=0 до х=2.
от х=0 до х=2.
 от х=0 до х=8.
от х=0 до х=8.
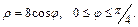

 , между точками пересечения с осями координат.
, между точками пересечения с осями координат.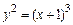 , отсекаемой прямой х=4.
, отсекаемой прямой х=4. от
от  до
до 
 от точки А(2,0) до точки В(6,8).
от точки А(2,0) до точки В(6,8).