Пояснения по выполнению лабораторной работы № 3.
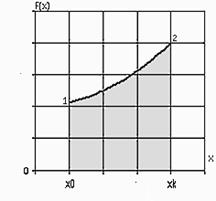
Определение площади лекала детали изделия. Имеется несколько способов определения площади лекала изделия. При геометрическом способе лекало разбивается на простые геометрические фигуры, площади которых легко определить по формулам. Площади фигур суммируются. Погрешность этого метода составляет 2–3% [3]. В таблице 4 приведены формулы вычисления площадей простых фигур. Площадь фигуры, ограниченной криволинейным контуром, можно подсчитать одним из методов численного интегрирования. Пусть требуется вычислить
Таблица 5.
Рис. 18. Пример (вычисление площади фигуры). Пусть требуется вычислить площадь приведенной на рисунке 18 фигуры. Для определения площади фигуры (рис. 18), следует определить площади двух фигур, одна из которых ограничена осью |

Создадим таблицу, в первой строке которой комментарии – имена переменных, а в первом столбце – номера точек (рис.19). В Excel площадь фигуры может быть вычислена следующим образом. В столбцы В и С рабочего листа введем координаты точек ломаной, ограничивающей фигуру. При этом будем записывать координаты, обходя фигуру по часовой стрелке. Для того чтобы ломаная была бы замкнута, координату начальной точки повторим дважды: в начале и в конце таблицы (рис. 19).
Вычисление площади фигуры начнем с вычисления площади первой трапеции. Её основания равны значениям  и
и  , записанным в ячейках С2 и С3. Высота трапеции представляет собой разность
, записанным в ячейках С2 и С3. Высота трапеции представляет собой разность  . Значение
. Значение  записано в ячейке В3, а
записано в ячейке В3, а 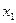 - в ячейке В2. Поскольку количество трапеций на единицу меньше количества точек, через которые проходит ограничивающая фигуру ломаная, для дальнейших вычислений ячейку D2 удобнее оставить пустой. Формулу, по которой вычисляется
- в ячейке В2. Поскольку количество трапеций на единицу меньше количества точек, через которые проходит ограничивающая фигуру ломаная, для дальнейших вычислений ячейку D2 удобнее оставить пустой. Формулу, по которой вычисляется  площадь первой трапеции, запишем в ячейке D3:
площадь первой трапеции, запишем в ячейке D3:
=0,5*(C3+C2)*(B3-B2) (*)

Рис. 19.
Щелкнув левой кнопкой мыши или нажав клавишу Enter, получим площадь первой трапеции. Выделим ячейку D3, поставим курсор мыши на маркер заполнения и протянем мышь вниз, не отпуская её кнопки, до ячейки D7. В ячейки D4÷D7 будет скопирована формула (*), выполнены вычисления. В этих ячейках появятся величины площадей остальных трапеций. Площадь всей фигуры получим после суммирования площадей всех трапеций с помощью кнопки «Автосуммирование» стандартной панели инструментов.
Обратите внимание на то, что в ячейках D6 и D7 значения  меньше нуля. Это не ошибка. Записывая координаты точек 1─5 (рис. 18), мы обходили фигуру по часовой стрелке. Поэтому высоты четвертой и пятой трапеций, вычисленные по формулам
меньше нуля. Это не ошибка. Записывая координаты точек 1─5 (рис. 18), мы обходили фигуру по часовой стрелке. Поэтому высоты четвертой и пятой трапеций, вычисленные по формулам  и
и 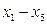 отрицательны.
отрицательны.

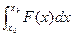 (рис. 17). Он равен площади фигуры, ограниченной осью х, кривой 1-2 и перпендикулярами, восстановленными из точек х0 и хк, т.е. площади криволинейной трапеции. Для вычисления этой площади разделим интервал интегрирования (отрезок [x0 xk]) на несколько частей (см. ри. 17.).
(рис. 17). Он равен площади фигуры, ограниченной осью х, кривой 1-2 и перпендикулярами, восстановленными из точек х0 и хк, т.е. площади криволинейной трапеции. Для вычисления этой площади разделим интервал интегрирования (отрезок [x0 xk]) на несколько частей (см. ри. 17.).


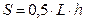



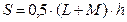

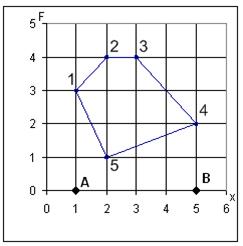
 и ломаной линией, проходящей через точки А,1, 2, 3, 4,В, а другая - той же осью
и ломаной линией, проходящей через точки А,1, 2, 3, 4,В, а другая - той же осью 


