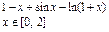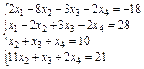Приближенные решения

Функция Minerr очень похожа на функцию Find (использует тот же алгоритм). Если в результате поиска не может быть получено дальнейшее уточнение текущего приближения к решению, Minerr возвращает это приближение. Функция Find в этом случае возвращает сообщение об ошибке. Правила использования функции Minerr такие же, как и функции Find.

Minerr(z 1, z 2 ,...)

Возвращает приближенное решение системы уравнений. Число аргументов должно быть равно числу неизвестных.

Если Minerr используется в блоке решения уравнений, необходимо всегда включать дополнительную проверку достоверности результатов.

Символьное решение уравнений

В Mathcad можно быстро и точно найти численное значение корня с помощью функции root. Но имеются некоторые задачи, для которых возможности Mathcad позволяют находить решения в символьном (аналитическом) виде.

Решение уравнений в символьном виде позволяет найти точные или приближенные корни уравнения:

· Если решаемое уравнение имеет параметр, то решение в символьном виде может выразить искомый корень непосредственно через параметр. Поэтому вместо того, чтобы решать уравнение для каждого нового значения параметра, можно просто заменять его значение в найденном символьном решении.

· Если нужно найти все комплексные корни полинома со степенью меньше или равной 4, символьное решение даст их точные значения в одном векторе или в аналитическом или цифровом виде.

Команда Символы Þ Переменные Þ Вычислить позволяет решить уравнение относительно некоторой переменной и выразить его корни через остальные параметры уравнения.

Чтобы решить уравнение символьно необходимо:

· Напечатать выражение (для ввода знака равенства используйте комбинацию клавиш [Ctrl]=).

· Выделить переменную, относительно которой нужно решить уравнение, щелкнув на ней мышью.

· Выбрать пункт меню Символы Þ Переменные Þ Вычислить.

Нет необходимости приравнивать выражение нулю. Если MathCAD не находит знака равенства, он предполагает, что требуется приравнять выражение нулю.

Чтобы решить систему уравнений в символьном виде, необходимо выполнить следующее:

· Напечатать ключевое слово Given.

· Напечатать уравнения в любом порядке ниже слова Given. Удостоверьтесь, что для ввода знака = используется [Ctrl]=.

· Напечатать функцию Find, соответствующую системе уравнений.

· Нажать [Ctrl]. (клавиша CTRL, сопровождаемая точкой). Mathcad отобразит символьный знак равенства ®.

· Щелкнуть мышью на функции Find.

Пример 2 Рисунка 4 иллюстрирует символьное решение системы уравнений в MathCAD.

Порядок выполнения практической работы 2

 

Упражнение 1. Построить график функции f (x)(Таблица 1) и приблизительно определить один из корней уравнения. Решить уравнение f (x) = 0с точностью e = 10 ^{– 4} с помощью встроенной функции Mathcad root;

Таблица 1

Варианты упражнения 1

№ вари-анта	f (x)	№ вари-анта	f (x)
			arccos - x х Î [2, 3]
			х 5 – х - 0,2 х Î [1, 2]

Упражнение 2. Для полинома g (x) (Таблица 2) выполнить следующие действия:

с помощью команды Символы Þ Коэффициенты полинома создать вектор V, содержащий коэффициенты полинома;

решить уравнение g (x) = 0 с помощью функции polyroots;

решить уравнение символьно, используя команду Символы Þ Переменные Þ Вычислить.

Таблица 2

Варианты упражнения 2

№ варианта	g (x)	№ варианта	g (x)
	x 4 - 2 x3 + x 2 - 12 x + 20		x 4 + x3 - 17 x 2 - 45 x - 100
	x 4 + 6 x3 + x 2 - 4 x - 60		x 4 - 5 x3 + x 2 - 15 x + 50
	x 4 - 14 x 2 - 40 x - 75		x 4 - 4 x3 - 2 x 2 - 20 x + 25
	x 4 - x3 + x 2 - 11 x + 10		x 4 + 5 x3 + 7 x 2 + 7 x - 20
	x 4 - x3 - 29 x 2 - 71 x -140		x 4 - 7 x3 + 7 x 2 - 5 x + 100
	x 4 + 7 x3 + 9 x 2 + 13 x - 30		x 4 + 10 x3 +36 x 2 +70 x + 75
	x 4 + 3 x3 - 23 x 2 - 55 x - 150		x 4 + 9 x3 + 31 x 2 + 59 x + 60
	x 4 - 6 x3 + 4 x 2 + 10 x + 75

Упражнение 3. Решить систему линейных уравнений (Таблица 3):

используя функцию Find;

матричным способом и используя функцию lsolve.

Таблица 3

Варианты упражнения 3

№ вари-анта	Система линейных уравнений	№ вари-анта	Система линейных уравнений

Упражнение 4. Преобразовать нелинейные уравнения системы из Таблицы 4 к виду f ₁(x) = y и f ₂ (y) = x. Построить их графики и определить начальное приближение решения. Решить систему нелинейных уравнений с помощью функции Minerr.

 

Таблица 4

Варианты упражнения 4

№ вари-анта	Система нелинейных уравнений	№ вари-анта	Система нелинейных уравнений

Упражнение 5. Символьно решить системы уравнений:

Контрольные вопросы

1. Назовите способы нахождения начального приближения.

2. Какие функции для решения одного уравнения в MathCAD вы знаете? В чем их отличие?

3. Какие аргументы функции root не обязательны?

4. В каких случаях MathCAD не может найти корень уравнения?

5. Какая системная переменная отвечает за точность вычислений?

6. Как изменить точность, с которой функция root ищет корень?

7. Как системная переменная TOL влияет на решение уравнения с помощью функции root?

8. Назовите функции для решения систем уравнений в MathCAD и особенности их применения.

9. Опишите структуру блока решения уравнений.

10. Какой знак равенства используется в блоке решения? Какой комбинацией клавиш вставляется в документ?

11. Какие выражения не допустимы внутри блока решения уравнения?

12. Опишите способы использования функции Find.

13. В каких случаях MathCAD не может найти решение системы уравнений?

14. Дайте сравнительную характеристику функциям Find и Minerr.

15. Какие уравнения называются матричными?

16. Как решать матричные уравнения? Назовите способы решения матричных уравнений.

17. Как символьно решить уравнение или систему уравнений в MathCAD? Какой знак равенства используется? Какой комбинацией клавиш вставляется в документ?

18. Назовите особенности использования символьного решения уравнений.