Коэффициент эластичности - показывает силу связи между переменными и является относительным показателем силы связи, поскольку выражен в процентах: .
Коэффициент эластичности показывает, на сколько процентов измениться в среднем результат, если фактор изменится на 1%.
Критерий F-Фишера - характеризует сопоставление факторной и остаточной дисперсии в расчете на одну степень свободы:. Лаг – число периодов, по которым рассчитывается коэффициент автокорреляции временного ряда. Линейная функция множественной регрессии -. Линейный коэффициент корреляции – показывает тесноту связи между признака и изменяется в пределах от -1 до 1. Чем ближе коэффициент корреляции по модулю к единице, тем теснее связь. Определяется по формуле. Метод наименьших квадратов для линейной парной регрессионной модели – параметры а и b находятся из систему уравнений . МНК для оценки параметров множественной линейной регрессии - для уравнения Множественная корреляция -практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата – коэффициента детерминации:. Множественная регрессия широко используется в решении проблем спроса доходности акций, при изучении функций издержек производства, в макроэкономический расчетах и целого ряда других вопросов эконометрики. Основная цель множественной регрессии – построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное воздействие их на моделируемый показатель. Модель временных рядов представляет собой зависимость результативного признака от переменной времени Мультиколлинеарность факторов - более чем два фактора связаны между собой в линейной зависимости, то есть имеет место совокупное воздействие факторов друг на друга. В результате вариация в исходных данных перестает быть полностью независимой и нельзя оценить воздействие каждого фактора в отдельности. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью МНК.
Модель временных рядов - данные, характеризующие один объект за ряд последовательных моментов времени. Мультипликативная модель временного ряда – временной ряд представлен как произведение циклической, трендовой и случайной компонент. Необходимое условие идентификации - выполнение счетного правила:D+1=H – уравнение идентифицируемо, D+1<H – уравнение неидентифицируемо, D+1>H – уравнение сверхидентифицируемо (Н – число эндогенных переменных в уравнении, D – число предопределенных переменных, отсутствующих в уравнении, но присутствующих в системе) Несмещенность оценки означает, что математическое ожидание остатков равно нулю. Если оценки обладают свойством несмещенности, то их можно сравнивать по разным исследованиям. Общая сумма квадратов отклонений Остаточная сумма квадратов: Парная регрессия представляет собой модель, где среднее значение зависимой (объясняемой) переменной у рассматривается как функция одной независимой (объясняющей) переменной х, то есть это модель вида: Показатели эластичности - показывают, на сколько процентов в среднем изменится результат, при изменении соответствующего фактора на 1 %. Предопределенные переменные – экзогенные и лаговые (за предыдущие моменты времени) эндогенные переменные системы. Приведенная форма модели - система линейных функций эндогенных переменных от всех предопределенных переменных системы: Регрессионные модели с одним уравнением – зависимая переменная представляется в виде функции Система взаимосвязных (совместных) уравнений – одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других – в правую Система независимых уравнений – каждая зависимая переменная у рассматривается как функция одного и того же набора факторов х: Система рекурсивных уравнений – зависимая переменная у одного уравнения выступает в виде фактора х в другом уравнении: Системы одновременных уравнений описываются системами взаимозависимых регрессионных уравнений. Совмещенные уравнения регрессии - к уравнениям, которые отражают не только влияние факторов, но и их взаимодействие, так если Состоятельность оценок характеризует увеличение их точности с увеличением объема выборки. Спецификация модели парной регрессии включает в себя следующие этапы: 1) выделение факторов, наиболее существенно влияющих на результативный признак; 2) уравнение простой регрессии характеризует связь между двумя переменными, которая проявляется как некоторая закономерность лишь по совокупности наблюдений. Практически в каждом отдельном случае величина у складывается из двух слагаемых: теоретического значения результативного признака и случайной величины, характеризующей отклонения реального значения результативного признака от теоретического – Стандартная ошибка коэффициента корреляции Стандартизованные коэффициенты регрессии показывают, на сколько единиц изменится в среднем результат, если соответствующий фактор Стандартная ошибка коэффициента регрессии рассчитывается по формуле Стандартная ошибка параметра а определяется по формуле Степенная функция множественной регрессии - Степень свободы – число возможных направлений варьирования признака. Существует равенство между числом степеней свободы общей, факторной и остаточной суммами квадратов: Сумма квадратов отклонений, обусловленных регрессией: Условие включения независимых переменных в уравнение множественной регрессии: матрица парных коэффициентов между ними была бы единичной, и имела бы определитель, равный единице: Фиктивные переменные – переменные, полученные путем перевода качественных признаков переменных в количественные, то есть присвоения им цифровых меток. Частные коэффициенты корреляции характеризуют тесноту связи между результатом и соответствующим фактором при элиминировании (устранении влияния) других факторов, включенных в уравнение регрессии. Частные коэффициенты эластичности позволяют определить эффекты влияния других факторов присоединены в них к свободному члену уравнения множественной регрессии Частные уравнения линейного уравнения множественной регрессии - уравнения регрессии, которые имеют следующий вид: Экзогенные переменные – независимые переменные, которые определяются вне системы х. Эконометрика – это самостоятельная научная дисциплина, объединяющая совокупность теоретических результатов, приемов, методов и моделей, предназначенных для того, чтобы на базе экономической теории, экономической статистики и экономических измерений, математико-статистического инструментария придавать конкретное количественное выражение общим (качественным) закономерностям, обусловленным экономической теорией. Экспоненциальная функция множественной регрессии - Эндогенные переменные – взаимосвязанные переменные, которые определяются внутри модели у. Этапы эконометрического исследования: 1) постановка проблемы, 2) получение данных, анализ их качества, 3) спецификация модели, 4) оценка параметров, 5) интерпретация результатов. Эффективность оценок - они характеризуются наименьшей дисперсией. В практических исследованиях это означает возможность перехода от точечного оценивания к интервальному.
|

 . МНК позволяет получить такие оценки параметров а и b при которых сумма квадратов отклонений фактических значений результативного признака от расчетных минимальна.
. МНК позволяет получить такие оценки параметров а и b при которых сумма квадратов отклонений фактических значений результативного признака от расчетных минимальна.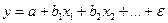 система нормальных уравнений составит:
система нормальных уравнений составит: 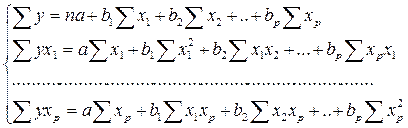 , ее решением может быть осуществлено методом определителей
, ее решением может быть осуществлено методом определителей 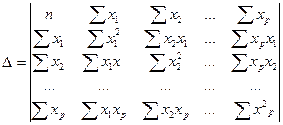
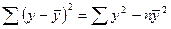 .
.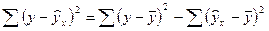 .
.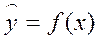
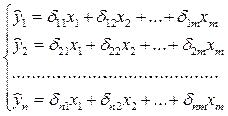
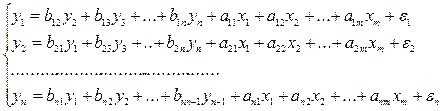


 , то можно построить совмещенное уравнение:
, то можно построить совмещенное уравнение: 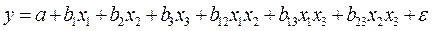 .
. ; 3) возмущение
; 3) возмущение 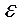 обусловлено тремя источниками: спецификацией модели, выборочным характером и особенностями измерения переменных. Каждый из данных источников может стать причиной ошибок, вследствие которых могут быть получены неверные выводы; 4) выбор вида математической функции; 5) построение графика линейной регрессии. Линейная регрессия сводится к нахождению уравнения вида:
обусловлено тремя источниками: спецификацией модели, выборочным характером и особенностями измерения переменных. Каждый из данных источников может стать причиной ошибок, вследствие которых могут быть получены неверные выводы; 4) выбор вида математической функции; 5) построение графика линейной регрессии. Линейная регрессия сводится к нахождению уравнения вида:  или
или 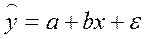 .
.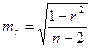 , фактическое значение величины t – критерия Стьюдента определяется как
, фактическое значение величины t – критерия Стьюдента определяется как 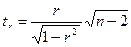 .
. изменится на одну единицу при неизменном среднем уровне других факторов.
изменится на одну единицу при неизменном среднем уровне других факторов. , фактическое значение t-критерия Стьюдента
, фактическое значение t-критерия Стьюдента 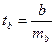 , которое сравнивается с табличным значением при определенном уровне значимости и числе степеней свободы (n-2). Доверительный интервал для коэффициента регрессии определяется как
, которое сравнивается с табличным значением при определенном уровне значимости и числе степеней свободы (n-2). Доверительный интервал для коэффициента регрессии определяется как 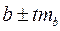
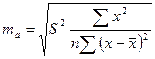 , t-критерий:
, t-критерий: 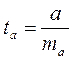 , его величина сравнивается с табличным значением при числе степеней свободы (n-2) и определенным уровнем значимости.
, его величина сравнивается с табличным значением при числе степеней свободы (n-2) и определенным уровнем значимости.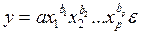 .
.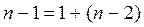 .
. .
.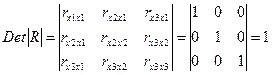 .
.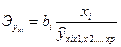 .
. ,
, 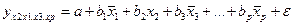 , ………………………………………….,
, ………………………………………….,  . При подстановке в эти уравнения средних значений соответствующих факторов они принимают вид парной регрессии:
. При подстановке в эти уравнения средних значений соответствующих факторов они принимают вид парной регрессии: 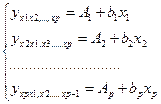 ,где:
,где: 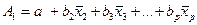 ,
, 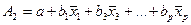 , ………………………………………….,
, …………………………………………., 
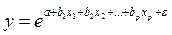 .
.


