Синтез кулачкового механизма
Задача заключается в проектировании кулачкового механизма с кулачком наименьших размеров по заданному закону перемещения толкателя. 4.5.1. Вариант 1. Кулачковый механизм с поступательно движущимся толкателем Здесь Н —максимальный ход толкателя; е —эксцентриситет; φ у —угол удаления толкателя; φнс — угол нижнего стояния толкателя; φп —угол приближения толкателя; φвс —угол верхнего стояния толкателя. Вариант 2. Кулачковый механизм с коромысловым толкателем 4.5.2. Построение закона движения толкателя Закон движения задается в виде диаграммы: Вариант 1,1а. S(φ) или a(φ). Вариант 2. Ψ(φ) или E(φ). 4.5.3. Построение диаграммы перемещения толкателя (или диаграммы ускорения толкателя). 1) Если задана диаграмма S(φ) (или Ψ(φ)), то построение начинаем сверху вниз и методом графического дифференцирования. Затем строим диаграммы V(φ) (или (W(φ)) и a(φ) (или (E(φ)). Диаграмму S(φ) (или Ψ(φ)), вычерчиваем следующим образом: А) Задаемся масштабом Б) Разбиваем ось (О φ) (240 мм) на четыре участка(φ у, φнс, φп, φвс.), согласно масштаба В) каждый из участков разбиваем пополам, таким образом, получаем 8 участков и дифференцируем каждый из них (см. рис. 33.). Аналогично в работе 1 (построение кинематических диаграмм). 2) Если задана диаграмма a(φ) (или E(φ)), то построение начинаем снизу вверх методом графического интегрирования, но прежде вычислив масштаб 4.5.4. Построение диаграммы плеч S(V) или Ψ(V) При построении S(V) (или Ψ(V)), используем метод исключения параметра (φ) из диаграмм S(φ) (или Ψ(V)) и V(φ) (или W(φ)). Для этого продолжаем оси обеих диаграмм вправо, затем проводим вертикальную ось, которая пересекает две оси в точках (О) и (О1). Через т. (О1) проводим, вспомогательную прямую N—N под углом 450. Кривые перемещения и скорости разбиваем на 8 точек по участка. Сносим параллельно первую точку диаграммы S(φ) (или Ψ(φ)), вправо. Из первой точки диаграммы скоростей V(φ) (или W(φ)) проводим линию параллельную горизонтали до пересечения с прямой N—N, получаем точку на этой прямой, из полученной точки проводим линию вертикально вверх. На пересечении двух линий получаем первую точку диаграммы плеч S(V) (или Ψ(V)). Аналогично проводим остальные 7 точек и соединяем плавной кривой линией. К полученной диаграмме плеч проводим касательные справа и слева под углом 300 к вертикали. На пересечении этих касательных получаем точку (К) и вниз от точки (К) — зону существования центров вращения кулачка. Отрезок (ОК) — дает минимальный радиус кулачка.
4.5.6. Построение теоретического и рабочего профиля кулачка 4.5.6.1.Вариант 1. Кулачковый механизм с поступательно движущимся толкателем В масштабе проводим окружность радиуса Rmin=(ОК). Из этого же центра проводим окружность радиуса е (эксцентриситет), эту окружность разбиваем на 8 равных частей, отмечаем 8 точек. Проводим касательную из крайней правой точки на окружности радиуса. Эта касательная отсекает на окружности радиуса Rmin т. (О). от данной точки отмечаем ординаты с диаграммы перемещения, получаем 8 точек. Из точек малой окружности проводим касательные, далее ставим ножку циркуля в центр вращения кулачка, точку (к). отмечаем расстояние (К1) и проводим дугу до т. (1). Аналогично строим остальные. Соединяем точки плавной кривой линией, получаем теоретический профиль кулачка. Перемещая ножку циркуля по теоретическому профилю кулачка, вычерчиваем семейство окружностей радиуса ролика
Список использованных литератур: 1. Теория механизмов и машин / методические указания и задания для выполнения курсовых работ. Монгуш Э. С. – Кызыл., Тувинский гос. университет, 2008. – 46 с. 2. Артоболевский И.И.. Теория механизмов и машин:Учеб. для втузов. – 4-е изд., перераб. и доп. – М.: Наука. Гл. ред. физ.-мат. лит., 1998. – 640 с. 3. Теория механизмов и машин: Учеб. для втузов/К.В. Фролов, С.А. Попов, А.К. Мусатов и др.; Под ред. К.В. Фролова. – М.: Высш. шк., 1987. – 496 с: ил. 4. Левитская О.Н., Левитский Н.И.. Курс теории механизмов и машин: Учеб. пособие для мех. спец. вузов. – 2-е изд., перераб. и доп. – М.: Высш. шк., 1985. – 279 с, ил. 5. Курсовое проектирование по теории механизмов и машин. Учеб. пособие / В.Н. Екшибаров, И.В.Левищев. – Барнаул: Изд-во Алтайского государственного аграрного университета, 2006. – 65 с, ил.
|



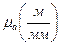 . Затем аналогично работе 2 (диаграмма работ А (φ)) произвести интегрирование.
. Затем аналогично работе 2 (диаграмма работ А (φ)) произвести интегрирование. . Проводим огибающую внутри семейства окружностей, получая рабочий профиль кулачка.
. Проводим огибающую внутри семейства окружностей, получая рабочий профиль кулачка.


