Под критическим состоянием трещины будем понимать момент страгивания и дальнейшее распространение (увеличение длины) трещины.
Произвольную объемную трещину можно представить в виде суперпозиции трех типов трещин, так называемых простых плоских трещин: I тип: трещина нормального отрыва (Рис. 4, А) Наиболее опасный и часто встречающийся тип. Например: процесс колки дров, дробление породы, бурение скважин, т.е. вбивание клина в любую поверхность; II тип: трещина поперечного сдвига (Рис. 4, Б). Данный вид трещины характерен практически при всех видах механической обработки; III тип: трещина продольного сдвига (Рис. 4, В). Например: скручивание образца с фасками, резание ножницами.
А Б В
Рис. 4. – Три типа трещин: А) Трещина нормального отрыва; Б) Трещина поперечного сдвига; В) Трещина продольного сдвига.
3. Теоретическая и реальная прочность твердых тел.
Теоретическая прочность может быть определена как прочность связей между атомами, ионами или другими структурными элементами, а также как химическая связь. Существуют различные модели оценки теоретической прочности тела. Выделим часть кристаллической решетки и рассмотрим взаимодействие двух рядом стоящих элементов (Рис.5) без учета влияния других элементов.
Рис. 5. – Взаимодействие двух элементов кристаллической решетки.
Попытка разрушения (смещения одного элемента относительно другого на расстояние x от первоначального равновесного положения
Рис. 6. – Реальная зависимость усилия
Проведем оценочный расчет величины
Рис. 7. – Аппроксимированная зависимость усилия
В этом случае изменение усилия взаимодействия частиц запишется так:
в силу того, что смещение мало (
проинтегрировав обе части уравнения (4.2) по
Если принять, что
Другие (аналогичные) оценки дают величину теоретической прочности в пределах
Оценка теоретической прочности материала дает величину, существенно превышающую значение реальной прочности (прочность, определяемая на образцах материала при испытаниях). Например: сталь Е~200 Гпа, В начале 20-х гг. российский физик-механник Иоффе провел эксперименты: был взят образец из каменной соли (монокристалл), который под действием растягивающей силы был разрушен. Затем такой же образец поместили в сосуд с горячим рассолом (водой) и довели до разрушения. Результат: прочность образца, помещенного в горячую воду, была в два раза выше, чем у образца, испытанного на воздухе. Вывод: при помещении образца в горячий рассол произошло залечивание поверхностных дефектов. Поверхностные дефекты являются инициаторами образования и дальнейшего распространения магистральных трещин. Следовательно, чем меньше поверхность образца, тем меньше вероятность образования поверхностного дефекта. Наименьшие по размерам образцы (усы) позволяют реализовать прочность соизмеримую с теоретической прочностью. Например, усы железа = 13.1 ГПа. Для повышения прочности необходимо стремиться к бездефектной структуре. Прочность, полученная при испытании обычных материалов по существующим ГОСТам, называется технической прочностью. Исследования по оценке теоретической прочности и опыты Иоффе показали необходимость изучения поведения материала с дефектами. Существенный прорыв в этой области был сделан Инглисом и Колосовым. Ими в 1909 г. была поставлена и решена задача о растяжении бесконечной пластины с эллиптическим отверстием (Рис. 8). Данная задача решалась методами функций комплексного переменного. Примем:
где

Рис. 8. – Бесконечная пластина с эллиптическим отверстием.
При Анализ решения Инглиса-Колосова и сопоставление его с реально существующей конструкцией позволил сделать следующие выводы: 1. Угловые точки, являясь концентраторами напряжений, служат источниками возникновения трещин; 2. Существующих феноменологических критериев (например 3. Внутренние и внешние дефекты, являясь концентраторами напряжений существенно уменьшают прочность материала и являются источниками микротрещин, которые приводят к разрушению. Исследования Иоффе и решения задач о концентрации напряжений наталкивают на мысль о том, что наличие трещин и различного рода трещиноподобных дефектов приводит к локальному ассимптотическому увеличению напряжений и вследствие этого к разрушению. Следовательно, необходим периодический осмотр объектов с целью выявления трещин с последующей заменой дефектных узлов или проведение мероприятий по «залечиванию» трещин.
4. Особенности разрушения композитов.
Одной из основных задач механики разрушения композиционных материалов является прогнозирование трещиностойкости, циклической и статической прочности композиционных материалов на основе известных свойств компонентов и проектируемой структуры материала. В силу наличия структуры в композитах существуют макро и микро подходы. В рамках макро подхода предполагается, что размер дефекта намного больше характерного размера элемента структуры, размер дефекта соотносится только с габаритами тела. На микро уровне предполагается, что композит изначально имеет дефектную структуру, эти дефекты являются источниками возникновения макротрещин. Неоднородность структуры и свойств приводит к накоплению рассеянных повреждений, вследствие этого к ухудшению макроскопических механических свойств. Изначально композиционные материалы имеют дефектные структуры. Эта дефектная структура является причиной ухудшения прочностных характеристик, и дефекты структуры являются инициаторами возникновения макротрещин. Наличие структуры предполагает наличие большого количества границ между компонентами. Это значительно улучшает прочностные свойства композиционных материалов в сравнении с однородными, за счет возможности торможения дефектов типа трещин на границе раздела фаз. За счет наличия структуры в композиционных материалах происходит локализация области концентрации напряжений. В однородных материалах при движении трещина не меняет своего типа, и в линейном механическом разрушении все критерии получены из этого предположения. В композитах трещина часто меняет тип.
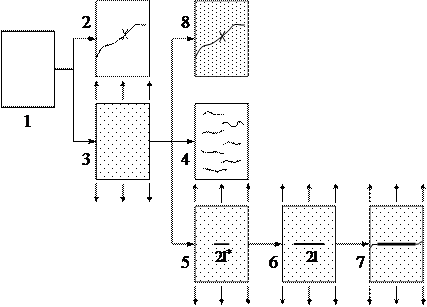
На Рис. 9 схематично показаны этапы разрушения композиционных материалов (предложены Болотиным В.В.).
Рис. 9. – Этапы разрушения композиционных материалов.
Где 1 – начальное состояние; 2 – хрупкое разрушение; 3 – накопление микроповреждений; 4 – разрушение вследствие потери целостности; 5 – образование макротрещины; 6 – рост макротрещины; 7 – финальное разрушение в результате роста макротрещины; 8 – хрупкое разрушение как результат накопления повреждений.
Реальные материалы разрушаются, как правило, по нескольким механизмам сразу. В силу изначальной дефектности структуры композиционного материала, в нем присутствует множество точек концентрации напряжений. Подобного типа задачи решаются с использованием только микромеханики с учетом реальной структуры материала. Данный тип задач используют при моделировании процессов разрушения. В случаях, когда рассматривается дефект, размеры которого много больше характерных размеров структуры, то для оценки концентрации напряжений могут быть использованы методы анизотропной механики. С использованием этих методов, в частности с использованием аналитического решение Колосова, решена задача о концентрации напряжений в эллиптическом отверстии (рис. 10) со следующими геометрическими характеристиками: m, n – угловые точки эллипса, В результате решения получаем максимальные напряжения в угловой точке m:
В угловой точке n:
где
Рис. 10. – Пластина с эллиптическим отверстием.
Из анализа видно, что на концентрацию напряжений влияет не только геометрия отверстия, но и упругие характеристики материала. Рассмотрим концентрацию напряжений в конкретных материалах (Рис. 11).
Рис. 11. – График зависимости концентрации напряжений от радиуса кривизны для различных материалов.
Где
|





 ) приведет к возникновению усилия, препятствующему этому; при этом усилие будет возрастать до определенной величины
) приведет к возникновению усилия, препятствующему этому; при этом усилие будет возрастать до определенной величины  , которую можно считать теоретической прочностью взаимодействия элементов.
, которую можно считать теоретической прочностью взаимодействия элементов.

 (4.1)
(4.1) )
) ; (4.2)
; (4.2) ;
;  ;
;  (4.3)
(4.3) получим:
получим: ;
; 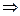
 ;
;  (4.4)
(4.4)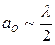 (размер равновесного состояния), то:
(размер равновесного состояния), то: . (4.5)
. (4.5) . В расчетах, при использовании термина ''теоретическая прочность'', принято брать значение
. В расчетах, при использовании термина ''теоретическая прочность'', принято брать значение 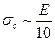 .
.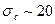 Гпа
Гпа  ~0,15
~0,15  0,2 Гпа. Т.е. реальная прочность минимум в двадцать раз меньше значения теоретической прочности. Возникает вопрос: почему не реализуется теоретическая прочность? Причина: дефекты и масштаб.
0,2 Гпа. Т.е. реальная прочность минимум в двадцать раз меньше значения теоретической прочности. Возникает вопрос: почему не реализуется теоретическая прочность? Причина: дефекты и масштаб. , (4.6)
, (4.6) - радиус закругления или радиус кривизны, а – большая ось эллипса, в - малая ось эллипса.
- радиус закругления или радиус кривизны, а – большая ось эллипса, в - малая ось эллипса.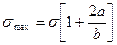 ; (4.7)
; (4.7)
 ; (4.8)
; (4.8) . (4.9)
. (4.9) – коэффициент концентрации напряжений, характеризующий увеличение напряжения в угловой точке, в зависимости от радиуса кривизны; показывает примерно во сколько раз максимальные напряжения в наиболее опасной точке больше, чем приложенные.
– коэффициент концентрации напряжений, характеризующий увеличение напряжения в угловой точке, в зависимости от радиуса кривизны; показывает примерно во сколько раз максимальные напряжения в наиболее опасной точке больше, чем приложенные. эллипс все больше приближается к трещине
эллипс все больше приближается к трещине  .
. ) недостаточно для оценки прочности конструкций, в которых либо существуют, либо возможно зарождение дефектов типа трещин;
) недостаточно для оценки прочности конструкций, в которых либо существуют, либо возможно зарождение дефектов типа трещин;

 . (4.10)
. (4.10) , (4.11)
, (4.11) – эффективные упругие параметры однородной анизотропной среды.
– эффективные упругие параметры однородной анизотропной среды.




