Требуемое число параллельных потоков будет
Полученное значение округляем до ближайшего целого, желательно четного, числа. Исходные данные для гидравлического расчета рабочего колеса будут:
2. РАСЧЁТ РАБОЧЕГО КОЛЕСА
2.1 Расчёт рабочих параметров ступени. 2.1.1.Вычисляем срывной кавитационный запас энергии. срывного кавитационного запаса энергии:
где
При подстановке в формулы численных значений следует обращать особое внимание на взаимное соответствие их размерностей. 2.1.2 Исходя из условия обеспечения безкавитационной работы, определяем максимальную скорость вращения вала насоса.
где
-для колёс нормальных кавитационных качеств -для колёс повышенных кавитационных качеств -для колёс высоких кавитационных качеств
2.1.3 Допустимая скорость вращения вала лежит в пределах:
2.1.4 Рабочая скорость вращения* вала принимается из условия
и должна согласовываться со скоростью вращения приводного двигателя и коэффициентом быстроходности. По коэффициенту быстроходности центробежные насосы делятся на три типа - тихоходные - нормальные - быстроходные Выбирая величину коэффициента быстроходности, надо помнить, что быстроходные колёса предназначены для создания малых напоров и больших производительностей, а колёса тихоходные используются для создания больших напоров и сравнительно малых производительностей. При постоянных значениях производительности и напора коэффициент быстроходности изменяется пропорционально скорости вращения вала и с увеличением последней увеличивается, что ведёт к уменьшению размеров и массы насоса. С увеличением
Тихоходные рабочие колёса имеют длинный и узкий межлопаточный канал и отношение Нормальные колёса имеют более короткий и широкий канал и отношение Быстроходные колёса имеют широкий и короткий канал и отношение Таким образом с точки зрения экономичности для заданных параметров следует применять колёса, соответствующие наибольшим значениям коэффициента быстроходности, т.к. при этом могут быть получены минимальные габариты и масса насоса. Однако это связано с повышением скорости вращения вала, которая лимитируется опасностью возникновения кавитации и увеличением диаметра вала, а также скоростью вращения приводного двигателя. Так как основным видом привода для судовых центробежных насосов служит в настоящее время электродвигатель, то максимальной скоростью вращения вала насоса при частоте 50Гц будет 314 1/с. Если в качестве привода используется паровая турбина (как правило, для привода питательных конденсатных и бустерных насосов), то скорость вращения может достигать 800 1/с и выше.
2.1.5. По выбранной скорости вращения вала и известным значениям и производительности ступени уточняют величину коэффициента быстроходности
где
2.1.6. Расчётный расход через рабочее колесо определяется по формуле
где 2.1.7.Для предварительного выбора объёмного к.п.д. можно пользоваться формулой, рекомендованной А.А.Ломакиным
Определённый таким образом объёмный к.п.д. учитывает лишь утечки через переднее уплотнение колеса. В многоступенчатых насосах имеются дополнительные утечки жидкости на систему разгрузки осевой силы, на смазку и охлаждение подшипников и т.п., которые составляют около 3-5%. Поэтому объёмный к.п.д. рекомендуется принимать предварительно из соотношения
2.1.8. Приведённый диаметр входа в колесо
Где
Рисунок 2.1.- Графики изменения параметров
2.1.9. Далее определяется теоретический напор колеса
где где Значения гидравлического к.п.д. выполненных колёс лежат в пределах
2.1.10. Мощность, потребляемая насосом, определяется из выражения
где
Величина к.п.д.
Величина к.п.д.
2.1.11.Максимальная мощность, потребляемая насосом при перегрузке будет
2.2. Расчёт основных размеров рабочего колеса на входе. Размеры входа рабочего колеса зависят в основном от производительности и рассчитываются из условия обеспечения требуемых кавитационных качеств и минимальных гидравлических потерь. 2.2.1 Скорость
где
Рисунок 2.2.-Схема меридианного сечения рабочего колеса
2.2.2 Диаметр вала колеса определяется в первом приближении из условий прочности на кручение
где
Крутящий момент на валу насоса будет
где Из условия обеспечения достаточной жёсткости вала нежелательно принимать диаметр его менее 20 мм.
2.2.3 Диаметр втулки колеса определяется конструктивно и в зависимости от диаметра вала и способа крепления колеса на валу принимается из соотношения
или
2.2.4 Диаметр входа в рабочее колесо
2.2.5 Ширина и расположение входной кромки лопасти зависит от кавитационных качеств насоса и коэффициента быстроходности ns и определяется из уравнения неразрывности
где D1 - диаметр окружности, проходящей через средние точки входных кромок лопастей. Этот диаметр выбирается для колёс нормальных и средних кавитационных качеств и низкой быстроходности из соотношения
Лопасти таких колёс выполняются цилиндрическими и входные кромки их располагаются либо параллельно оси насоса, либо под углом 15-30° к оси. В колёсах высоких кавитационных качеств и колёсах высокой быстроходности входная кромка лопасти сильно выдвигаются в область поворота потока из осевого направления в радиальное и диаметр D1 выбирается из соотношения
Для судовых насосов, если нет специальных требований, чаще всего принимают
2.2.6 Меридианная составляющая абсолютной скорости на входе с учётом стеснения потока лопастями будет
где
2.2.7 Окружная скорость жидкости на входе в рабочее колесо
Рисунок 2.3- Треугольники скоростей на входе в рабочее колесо насоса
2.2.8 Угол безударного входа потока на лопасти определяется из соотношения скоростей
2.2.9 Угол установки лопасти на входе будет b1=b1,0+d, где d - угол атаки, принимаемый в пределах - для колёс нормальных кавитационных качеств
- для колёс повышенных и высоких кавитационных качеств
а в специальных случаях до 25°. Большие значения На основании анализа размеров колёс насосов, обеспечивающих наиболее высокие значения гидравлического к.п.д. А.А.Ломакин рекомендует принять угол установки лопасти на входе в пределах
2.2.10 Относительная скорость на входе
2.3 Расчёт основных размеров колеса на выходе.
2.3.1 Окружная скорость на выходе из рабочего колеса в первом приближении вычисляется по формуле
где
2.3.2 Наружный диаметр колеса в первом приближении будет
2.3.3 Угол установки лопасти на выходе из колеса b2 можно определить следующим образом
где
Значение
Обычно, если нет каких-либо специальных соображений, принимают Для обеспечения устойчивого движения жидкости в каналах колеса желательно принимать отношение
Среднестатистическое значение оптимального угла b2 на выходе из колеса из условия получения максимального к.п.д. находится в пределах Нижним пределом для колеса с точки зрения экономичности и стеснения канала лопатками на входе является угол Относительная скорость на выходе
Рисунок 2.4 - Треугольники скоростей при выходе из рабочего колеса
2.3.4 Наивыгоднейшее число лопастей по данным обследования колёс с высоким к.п.д. можно получить по формуле
где 6,5 - опытный коэффициент.
Большинство выпускаемых в настоящее время центробежных насосов с высокими технико-экономическими показателями независимо от размеров и коэффициента быстроходности ns имеют рабочие колёса с числом лопастей z= 6÷8. При числе лопаток более 9 производят подрезку лопаток на входе через одну (примерно, на 1/4 длины). 2.3.5 Теоретический напор, создаваемый колесом при бесконечно большом числе лопастей, определяется по формуле
где p - поправка Пфлейдерера на конечное число лопастей, вычисляемая по формуле Величину коэффициента
Величина первого слагаемого в этой формуле зависит от степени шероховатости проточной части и типа отвода потока от колеса. Для тщательно обработанных колёс и лопаточных отводов эта величина принимается меньше, а для литых колёс и спиральных отводов - больше. Поправка Пфлейдерера даёт хорошее совпадение с опытными данными для колёс с ns £150 c лопастями загнутыми назад. 2.3.6 Окружная скорость потока на выходе из рабочего колеса во втором приближении определится из выражения, полученного в результате преобразования основного уравнения лопастных насосов
2.3.7 Наружный диаметр колеса во втором приближении
Если величина наружного диаметра колеса во втором приближении отличается от величины, полученной в первом приближении не более, чем на 5%, то значение D2, полученное во втором приближении, можно считать окончательным. Если же отличие составляет более 5%, то необходимо сделать третье приближение, для чего нужно повторить расчёт, начиная с пункта 2.3.4 и подставляя вместо D2 его численное значение, полученное во втором приближении. Получив значение D2 в третьем приближении, сравнивают его со значением, полученным во втором приближении. Расхождение между двумя соседними приближениями не должно превышать 5%. 2.3.8 Ширина канала на выходе из рабочего колеса определится из уравнения неразрывности
Для получения высокого значения к.п.д. необходимо выполнение условия 2.4 Расчёт и построение меридианного сечения канала колеса. Профилирование канала в меридианном сечении делается таким образом, чтобы получить плавный переход от величины меридианной составляющей абсолютной скорости Для каждого значения
Рисунок 2.5- График изменения меридианной составляющей абсолютной скорости в зависимости от радиуса
Расчёт удобно вести в табличной форме
Таблица 2.1
Приращение радиуса при расчёте следует принимать равным 5-10 мм. Форма меридианного сечения тихоходного колеса вытянута в радиальном направлении. Контур канала колеса по несущему диску от выхода к входу выполняется нормально к оси и плавно округляется при переходе от радиального направления к осевому. Скругление желательно выполнять по квадратичной параболе (рис 2.6). Контур канала колеса по покрывающему диску строится как огибающая окружностей, описанных радиусами Этим же методом профилируют и меридианное сечение колёс нормальной быстроходности при малом угле наклона основного диска к оси (до 5°).
Рисунок 2.6- К построению меридианного сечения канала рабочего колеса
В быстроходных колёсах входная кромка выдвинута во входное отверстие, а лопасти представляют собой поверхности двоякой кривизны. Основной диск от наружного диаметра выполняют или прямым под углом к вертикали 5…120 с плавным округлением у втулки или криволинейным (Рис.2.7). Форму контура покрывающего диска определяют также, как и для тихоходных колёс. Так как меридианные сечения быстроходных колёс имеют большую ширину, то их разбивают на элементарные колёса с равными расходами. В первом приближении положение линий тока и нормальных линий намечают на глаз. Начинают с разбивки вертикали входного отверстия диаметрами Di на 3-5 частей (рис.2.7) из условия равенства расхода через площади кольцевых сечений, что соответствует условию
где n - число элементарных колёс. Выходную кромку лопасти b2 разбивают на такое же число равных частей. Линии тока 2-2, 3-3, 4-4 (рис.2.7) проводят на глаз. На определённом расстоянии к этим линиям проводят нормали. Положение линий тока 2-2, 3-3, 4-4 уточняют, начиная с входной кромки. Для этого на чертеже замеряют радиусы Ri центров тяжести нормалей между линиями токов и ширину Dbi и составляют таблицу 2.2, из которой определяют ошибку d (Dbi) и уточняют ширину элементарного колеса.
Таблица 2.2
Рисунок 2.7- План построения меридианного сечения быстроходного колеса
Последовательным приближением уточняют положение линий тока от входной кромки к выходу, делящих канал колеса в меридианном сечении на элементарные колёса с разными расходами. d(Ri ×Dbi) =
2.5 Расчёт и построение цилиндрической лопасти в плане. Сечение лопасти в плане строится по средней линии и толщине лопасти D. Средняя линия делит пополам толщину лопасти, откладываемую по нормали к средней линии. Средняя линия профиля лопасти в плане строится по точкам, положение которых определяется радиусом R и углом
При сильно изогнутом меридианном сечении рабочих колёс (сильно изогнутой линии тока) вместо dR следует принимать отрезок по линии тока dx (рис.2.I0). При этом принято, что при R=R1 q=0. Угол установки лопасти на любом радиусе находится по формуле
Интегрирование выражения (2.1) производится приближённо по правилу трапеций, так как угол
Расчёт координат R и q средней линии профиля в плане рекомендуется вести в табличной форме (табл.2.3). Относительная скорость жидкости в каналах колеса
Рисунок 2.8. К расчёту профиля цилиндрической лопасти в плане
Рисунок 2.9. График зависисмости относительной скорости жидкости от радиуса
Меридианная составляющая абсолютной скорости Толщина лопасти на входе D1 и на выходе D2 определяются по формулам
где
Шаг лопастей определяется по формулам
Максимальная толщина лопасти принимается в зависимости от размеров колеса, технологии изготовления и материала равной Dmax =3÷8 мм в средней части сечения или ближе к верхней кромке. Бронзовые колёса могут быть с более тонкими лопатками, чем стальные.
Рисунок 2.10. Зависимость толщины лопасти от радиуса
1-криволинейная зависимость; 2- линейная зависимость.
По координатам R и q строится средняя линия сечения лопасти в плане. Из точек на средней линии, соответствующих расчётным радиусам, как из центров проводятся окружности диаметром, равным толщине лопасти D на данном радиусе. Затем проводится огибающая этих окружностей, которая и будет контуром сечения лопасти в плане. Входная и выходная кромки лопасти закругляются соответственно по радиусам
Таблица 2.4
Поверхность лопасти двоякой кривизны строится по отдельным сечениям лопасти поверхностями тока, представляющими собой поверхности вращения. Форма сечения лопасти двоякой кривизны определяется также двумя проекциями: на меридианной плоскости и в плане. Профилирование лопастей быстроходных рабочих колёс, разбиваемых на несколько элементарных колёс, принципиально не отличается от рассмотренного, но его удобнее проводить от внешнего радиуса к внутреннему [10]. Подробно методика расчёта и построение поверхности пространственной лопасти изложена в работах [2], [3], [6], [10] и др.
3 РАСЧЁТ ОТВОДЯЩЕГО УСТРОЙСТВА 3.1 Выбор типа отводящего устройства. Назначение отводящего устройства центробежного насоса состоит в том, чтобы собрать жидкость, выходящую из каналов рабочего колеса, и отвести её к выходному патрубку насоса. При этом отводящие устройства должны -обеспечить осесимметричность потока жидкости за рабочим колесом и тем самым создать условия для установившегося относительного движения жидкости в рабочем колесе; -преобразовать кинетическую энергию потока, выходящего из рабочего колеса, в энергию давления. В отводящих устройствах центробежных насосов в потенциальную энергию давления преобразуется около 30% энергии, сообщаемой жидкости в рабочем колесе. Поэтому их гидравлическое совершенство существенно сказывается на к.п.д. насоса. В центробежных насосах применяются отводящие устройства двух типов: спиральные отводы и направляющие аппараты (лопаточные отводы). Различие между ними состоит в конструктивном исполнении и технологии изготовления. С точки зрения гидравлики спиральному отводу можно придать более совершенную обтекаемую форму, но каналы его недоступны механической обработке, поэтому форма, размеры и чистота их поверхности должны обеспечиваться непосредственно в отливке. Каналы направляющих аппаратов имеют в поперечном сечении прямоугольную форму, принципиально менее благоприятную в гидравлическом отношении, но пригодную для механической обработки. Поскольку при небольших абсолютных размерах каналов чистота поверхности и отклонение от теоретической формы существенно сказываются на гидравлических свойствах каналов, то в конечном итоге механически обрабатываемые лопаточные отводы обеспечивают лучшие гидравлические качества. Однако, спиральные отводы значительно проще по конструкции и дешевле в изготовлении. Поэтому целесообразность применения спирального или лопаточного отвода в первую очередь зависит от совершенства технологии литья. Спиральные отводы имеют лучшие конструктивные и технико-экономические показатели в одно- двухступенчатых насосах, тогда как лопаточные отводы, благодаря более высоким гидравлическим качествам и значительно меньшим размерам, получили преимущественное распространение в многоступенчатых высоконапорных насосах. В последнее время, в связи с совершенствованием технологии литейного производства, спиральные отводы стали применять и в многоступенчатых насосах, однако в этом случае сильно увеличиваются габариты насоса.
3.2 Расчёт спирального отвода произвольного сечения. Поперечное сечение спирального канала может иметь различную форму. Оно может быть круглым (рис.3.1а), очерченным по дуге круга и двум прямым, касательным к дуге и образующим в пересечении угол 20÷30° (рис.3.1б) и в виде сектора со скруглёнными углами (рис.3.1в). Результаты исследований, выполненных на кафедре ССУ СПИ свидетельствуют о том, что поперечные габариты судовых центробежных насосов могут быть значител
|


 и
и  .
.
 ,
, – упругость паров жидкости при заданной температуре, Па;
– упругость паров жидкости при заданной температуре, Па; - плотность жидкости при заданной температуре,
- плотность жидкости при заданной температуре,  ;
; – ускорение силы тяжести,
– ускорение силы тяжести,  ;
; - коэффициент запаса, который согласно ГОСТ 6134-71 принимается в пределах
- коэффициент запаса, который согласно ГОСТ 6134-71 принимается в пределах  ,
, – производительность ступени в
– производительность ступени в  ;
; - кавитационный коэффициент быстроходности, величина которого принимается в зависимости от назначения и требуемых кавитационных качеств насоса. Ориентировочно можно принимать
- кавитационный коэффициент быстроходности, величина которого принимается в зависимости от назначения и требуемых кавитационных качеств насоса. Ориентировочно можно принимать =800-1000;
=800-1000; ,
, ,
, =50-80;
=50-80; ) и увеличивается его осевая ширина (d).
) и увеличивается его осевая ширина (d).
 ,
, ;
; - напор ступени,
- напор ступени, 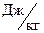 ;
; - скорость вращения вала,1/с.
- скорость вращения вала,1/с. ,
, - объёмный к.п.д., значение которого находится в пределах
- объёмный к.п.д., значение которого находится в пределах  .
. ,
, ,
, , м находится из уравнения подобия
, м находится из уравнения подобия ,
, - коэффициент, величина которого лежит в пределах
- коэффициент, величина которого лежит в пределах  = 3,6-6,5 и выбирается в зависимости от кавитационного коэффициента быстроходности
= 3,6-6,5 и выбирается в зависимости от кавитационного коэффициента быстроходности 

 в зависимости от
в зависимости от  ,
, ,
, - гидравлический к.п.д., величина которого в первом приближении может быть определена по формуле, предложенной А.А.Ломакиным
- гидравлический к.п.д., величина которого в первом приближении может быть определена по формуле, предложенной А.А.Ломакиным ,
, - приведённый диаметр входа колеса в мм.
- приведённый диаметр входа колеса в мм. ,
,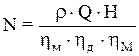 ,
, - механический к.п.д. насоса, равный
- механический к.п.д. насоса, равный ,
, , учитывающего потери энергии на трение колеса о воду (дисковое отношение), может быть определена из выражения
, учитывающего потери энергии на трение колеса о воду (дисковое отношение), может быть определена из выражения ,
, , учитывающего потери энергии на трение в сальниках и подшипниках, лежит в пределах
, учитывающего потери энергии на трение в сальниках и подшипниках, лежит в пределах  ,
, на входе в рабочее колесо, соответствующую минимальному динамическому падению давления, можно определить по формуле, предложенной С.С.Рудневым
на входе в рабочее колесо, соответствующую минимальному динамическому падению давления, можно определить по формуле, предложенной С.С.Рудневым ,
, - коэффициент, величина которого лежит в пределах
- коэффициент, величина которого лежит в пределах 
 ,
, , Н/м
, Н/м  - допускаемое напряжение на кручение, принимаемое для стальных валов в пределах
- допускаемое напряжение на кручение, принимаемое для стальных валов в пределах =(2000-5000)×104,
=(2000-5000)×104, ,
, - потребляемая мощность в Вт.
- потребляемая мощность в Вт. ,
, ,
, ,
, ,
,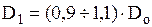 ,
, ,
, - меридианная составляющая абсолютной скорости на входе в рабочее колесо без учёта стеснения потока лопастями. Значение её принимается из соотношения:
- меридианная составляющая абсолютной скорости на входе в рабочее колесо без учёта стеснения потока лопастями. Значение её принимается из соотношения: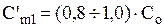 - для колёс низкой быстроходности и нормальных и средних кавитационных качеств.
- для колёс низкой быстроходности и нормальных и средних кавитационных качеств. - для колёс повышенной быстроходности высоких кавитационных качеств.
- для колёс повышенной быстроходности высоких кавитационных качеств. .
. ,
, - коэффициент стеснения на входе, принимаемый в пределах
- коэффициент стеснения на входе, принимаемый в пределах  . Значением этого коэффициента задаются, а после определения угла b1 его уточняют.
. Значением этого коэффициента задаются, а после определения угла b1 его уточняют. ,
,
 ,
, ,
,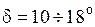 ,
, принимают также при малых углах b1,0.
принимают также при малых углах b1,0. ,
, ,
, ,
, - коэффициент окружной составляющей абсолютной скорости на выходе из рабочего колеса, принимаемый в пределах
- коэффициент окружной составляющей абсолютной скорости на выходе из рабочего колеса, принимаемый в пределах  .
.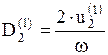 ,
, ,
, - коэффициент стеснения потока лопастями на выходе из рабочего колеса, принимаемый в пределах
- коэффициент стеснения потока лопастями на выходе из рабочего колеса, принимаемый в пределах  ; окончательно он принимается после определения угла b2;
; окончательно он принимается после определения угла b2; - меридианная составляющая абсолютной скорости на выходе из рабочего колеса без учёта стеснения потока лопастями.
- меридианная составляющая абсолютной скорости на выходе из рабочего колеса без учёта стеснения потока лопастями. -для колёс нормальных кавитационных качеств (
-для колёс нормальных кавитационных качеств ( );
); );
); .
. ,
,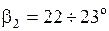 независимо от значения
независимо от значения  . В специальных случаях, когда требуется обеспечить получение высокого напора при минимальных размерах колеса, угол b2 может быть увеличен до 45÷50°.
. В специальных случаях, когда требуется обеспечить получение высокого напора при минимальных размерах колеса, угол b2 может быть увеличен до 45÷50°.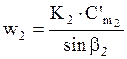 ,
,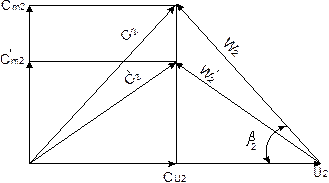

 ,
, ,
, находят из выражения
находят из выражения ,
, ,
, ,
, ,
, .
. на входе к её значению
на входе к её значению  на выходе. Для этого задаются графиком изменения скорости
на выходе. Для этого задаются графиком изменения скорости  . При этом, как правило, принимают линейный закон изменения скорости
. При этом, как правило, принимают линейный закон изменения скорости 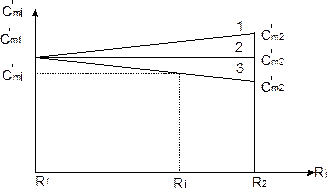
 ;
;  ;
; 



 с центрами на соответствующих Ri и касательных к контуру канала по основному (несущему) диску (рис.2.6). Для более плавного изменения контура канала по покрывающему диску в месте перехода из радиального направления в осевое входную кромку под углом 15…30° к оси.
с центрами на соответствующих Ri и касательных к контуру канала по основному (несущему) диску (рис.2.6). Для более плавного изменения контура канала по покрывающему диску в месте перехода из радиального направления в осевое входную кромку под углом 15…30° к оси.
 =
=  =
=  =
=  =
= 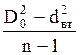 ,
,

 ,
, (рис.2.8). Координаты средней линии Ri и
(рис.2.8). Координаты средней линии Ri и  находится из уравнения линии тока
находится из уравнения линии тока , (2.1)
, (2.1) ,
, , толщина лопасти D и скорость
, толщина лопасти D и скорость  и
и  задаются в виде графиков в функции от радиуса. Обозначив подинтегральную функцию как
задаются в виде графиков в функции от радиуса. Обозначив подинтегральную функцию как  , получим для промежуточного угла, соответствующего радиусу
, получим для промежуточного угла, соответствующего радиусу  , следующее выражение
, следующее выражение ,
, если зависимость
если зависимость  изгибается вверх (рис.2.9-пунктир), то лопасть удлиняется, если вниз- укорачивается.
изгибается вверх (рис.2.9-пунктир), то лопасть удлиняется, если вниз- укорачивается.

 , которые соединяются между собой так, чтобы обеспечить плавное изменение толщины лопасти от радиуса
, которые соединяются между собой так, чтобы обеспечить плавное изменение толщины лопасти от радиуса  до радиуса
до радиуса  .
. , (не должна быть менее 2,5 мм)
, (не должна быть менее 2,5 мм) , (не должна быть менее 1,5 мм)
, (не должна быть менее 1,5 мм) и
и  - соответственно коэффициенты стеснения потока лопастями на входе и на выходе из рабочего колеса;
- соответственно коэффициенты стеснения потока лопастями на входе и на выходе из рабочего колеса; и
и  - соответственно шаг лопастей на радиусе
- соответственно шаг лопастей на радиусе  ,
,  .
.
 и
и  . Желательно, чтобы угол обхвата лопасти в плане qЛ лежал в пределах qЛ = 80÷120°.
. Желательно, чтобы угол обхвата лопасти в плане qЛ лежал в пределах qЛ = 80÷120°.









