КОЭФФИЦИЕНТА ЗАПОЛНЕНИЯ kС И ИЗОЛЯЦИОННЫХ РАССТОЯНИЙ НА МАССУ И СТОИМОСТЬ АКТИВНЫХ МАТЕРИАЛОВ ТРАНСФОРМАТОРА
Расчет отдельного трансформатора обычно проводится на базе существующей серии трансформаторов с определенными конструкциями магнитных систем и обмоток, общей для всей серии конструкцией изоляции, установленными изоляционными расстояниями, известными марками активных и изоляционных материалов и общей технологией производства. В этом случае параметры короткого замыкания Р K и uK l , входящие в ряд параметров всей серии, коэффициент заполнения площади круга активным сечением стержня k C, определяемый выбранной маркой стали и принятой технологией изготовления магнитной системы, и изоляционные расстояния главной изоляции обмоток, зависящие от конструкции главной изоляции и применяемых изоляционных материалов, по существу являются заданными для расчетчика. При разработке новых серий обычно производится изменение, как конструкции, так и технологии производства трансформаторов, применяются новые, более эффективные или экономичные магнитные, проводниковые и изоляционные материалы, улучшаются параметры трансформаторов серии. При этом обычно стремятся уменьшить потери холостого хода Р X и короткого замыкания Р K, увеличить коэффициент заполнения k C и уменьшить не в ущерб электрической прочности трансформатора изоляционные расстояния главной изоляции обмоток. Для оценки эффективности подобных изменений необходимо исследовать, как эти изменения отражаются на параметрах трансформатора, массах и стоимости его активных материалов. Изменение потерь короткого замыкания трансформатора может быть произведено изменением плотности тока в обмотках и соответствующим изменением массы металла обмоток. Массу металла обмоток, как было показано ранее (см. § 11.1), можно определить по формуле Из величин, входящих в это выражение, от потерь короткого замыкания Р K зависит только ua = P K(10S). Косвенно от Р K> зависит параметр а, принимаемый постоянным для заданных потерь Р K> , но изменяющийся при изменении Р K> (см. § 3.5 и табл. 3.4). Таким образом, G0~C1~a2/PK (11.7) При относительно небольших изменениях Р K — в пределах ±20 % можно считать a = const и пользоваться упрощенной формулой G0~1/PK (11.8) Изменение плотности тока с изменением РК можно получить из (3.60) или, если пренебречь изменением а, J~PК (11.10) Зависимости между G0, J и РК графически изображены на рис. 11.5 сплошными линиями для упрощенных формул (11.8) и (11.10) и штриховыми линиями для точных формул (11.7) и (11.9). При этом за 100% приняты значения G0, J и РК для любого исходного известного варианта. В связи с некоторым изменением сечения обмоток и необходимостью изменения площади окна магнитной системы при изменении РК несколько изменится масса стали GCT—
Рис. 11.5. Зависимость между потерями короткого замыкания РК, массой металла обмоток G0 и плотностью J 1 и 2-по (П.8) и (11.10); 3 и 4- по style='mso-bidi-font-size7.0pt'>(11.7) и (11.9)
Рис. 11.6. Изменение массы стали GCT, стоимости активной части Са,ч и увеличивается с уменьшением Р K и уменьшается с его увеличением. Графики на рис. 11.5 показывают, что при изменениях Р K в пределах ±20 % можно с успехом пользоваться упрощенными формулами. Из кривой 1 следует также, что уменьшение потерь короткого замыкания путем уменьшения плотности тока сопряжено с существенным увеличением массы металла обмоток. Коэффициент заполнения сталью k C, равный произведению двух коэффициентов kKP — коэффициента заполнения круга и k3 — коэффициента заполнения сечения стержня, входит в число исходных данных, выбираемых до начала расчета трансформатора. От значения коэффициента k C зависят коэффициенты А (3.30), А1 (3.35), В1 (3.43) и С1 (3.52), а именно A ~ B1 ~ A3kC ~ Коэффициенты A2 и B2 от kС не зависят А 2 ~ A2kС ~ Из приведенных зависимостей следует, что с ростом kС уменьшается масса стали GCT (А1 и B1) и масса металла обмоток (С1), а вместе с ними стоимость активных материалов, потери и ток холостого хода при сохранении неизменных значений РК и uK, положенных в основу рассматриваемых выражений. Коэффициент k3 зависит от толщины выбранной марки стали (0,35; 0,30 или 0,27 мм) и вида изоляции пластин. Современная холоднокатаная сталь с нагревостойким электроизоляционным покрытием ЭТ (ГОСТ 21427-83) имеет коэффициент заполнения для этих толщин соответственно k3=0,97-0,94 и без покрытия не более 0,97. Следовательно, коэффициент заполнения сечения стержня k3 не дает реальной возможности для увеличения k C. Коэффициент заполнения круга kKP зависит от числа и размеров.ступеней (пакетов) в сечении стержня. Увеличение числа ступеней с уменьшением толщины пакетов позволит увеличить kK P, однако усложнит технологию изготовления магнитной системы. Ограниченные возможности увеличения коэффициента kKP для диапазона диаметров стержня от 0,08 до 0,75 м рассмотрены в § 8.1. Основные изоляционные расстояния главной изоляции обмоток — ширина канала между обмотками ВН и НН а12, расстояние от обмотки ВН до ярма l0 и расстояние между обмотками ВН соседних фаз а22 — в явном виде входят в формулы (3.36) и (3.44), определяющие массу стали магнитной системы, а расстояние а12 в скрытом виде входит также в выражение (3.30), служащее основой системы обобщенного расчета магнитной системы и обмоток. Влияние размеров изоляционных расстояний на массу активной части сказывается в большей степени в трансформаторах с более высоким номинальным напряжением обмоток ВН, а в трансформаторах с одинаковыми номинальными напряжениями— при относительно меньших мощностях. При проектировании новых серий всегда стремятся уменьшить изоляционные расстояния применением новых материалов, обладающих повышенной электрической прочностью, и новых улучшенных изоляционных конструкций или снижением испытательных напряжений. Во всех этих случаях представляется интересным оценить, в какой степени является эффективным то или иное мероприятие по уменьшению изоляционных расстояний. Исследование этого вопроса проведено путем расчета по обобщенному методу нескольких вариантов трехфазного двухобмоточного трансформатора типа ТДН-25000/110 мощностью 25 000 кВ·А с напряжением обмотки ВН ПОкВ. Расчет производился по методике, описанной в § 3.5 и 3.6 для пяти вариантов изоляционных расстояний a12, l0 и а22, составляющих 70, 80, 90, 100 и 110 % соответствующих расстояний в серии трансформаторов с напряжением ВН 110 кВ. При расчете была принята сталь марки 3404 толщиной 0,35 мм по ГОСТ 21427-83 при неизменных потерях короткого замыкания Р K и uK= 10,5 %. Изменение а12 отражается при расчете на коэффициентах А, А1, А2, В1, В2 и С1. Кроме того, коэффициенты А2 и В2 зависят также от l0 и от а12 и а22- Поэтому в результате расчетов были получены варианты трансформаторов с различными массами стали GCT и металла обмоток G0. При этом уменьшение изоляционных расстояний при сохранении одного значения Поскольку увеличение массы металла обмоток является нежелательным, были подобраны такие значения Результаты расчетов представлены в виде кривых на рис. 11.6. Снижение изоляционных расстояний на 20—30 % по сравнению с расстояниями в реальном трансформаторе типа ТДН-25 000/110 может привести к снижению массы стали, а следовательно, и потерь холостого хода на 7—10 % и стоимости активной части на 3—4 %. С увеличением мощности трансформатора при сохранении напряжения обмотки ВН 110 кВ эффект от уменьшения изоляционных расстояний будет соответственно уменьшаться.
|


 (11.9)
(11.9)

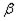 с изменением изоляционных расстояний а12, l0, а22 (Р K== const; uK = const; G0= const)
с изменением изоляционных расстояний а12, l0, а22 (Р K== const; uK = const; G0= const) ; A1 ~ A3kC ~
; A1 ~ A3kC ~  ~
~ 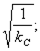
 ~
~  ~
~ 
 ~ 1; B2 ~ A2kС ~ 1.
~ 1; B2 ~ A2kС ~ 1.


