РОЗВ’ЯЗАННЯ ЗАДАЧІ КОМІВОЯЖЕРА ЗА ДОПОМОГОЮ ГЕНЕТИЧНОГО АЛГОРИТМУ
3.1 Вибір та обґрунтування форми подання задачі В першу чергу розпочнемо із зручного представлення шляху комівояжера (туру). Міста, які будуть входити в певний шлях, який буде пройдений комівояжером представимо у формі масиву фіксованого розміру Tour. Масив Tour буде містити елементи (Tour1, Tour2, …, Tourn-1, Tourn), де Tour1, Tour2, …, Tourn-1, Tourn – це можливі варіанти шляху комівояжера. Таким чином будемо мати двомірний масив турів, в кожен з яких буде входити впорядкований набір міст. Таке представлення надзвичайно вигідне з точки зору програмної реалізації, оскільки в подальшому будемо використовувати як приклад операцію сортування на основі функції відповідності, яка в даному представленні зведеться до впорядкування елементів масиву. Щодо вартостей шляхів (турів) комівояжера, то в даному випадку будемо вводити масив TourCost, в плані розмірності, який буде ідентичний масиву Tour. Також потрібно зауважити що масиви повинні бути зв’язані між собою суворою відповідністю: Tour1 → TourCost1, Tour2 → TourCost2,…, Tourn→ TourCostn. Далі буде здійснюватися процедура сортування, а саме сортування за критерієм вартості шляху комівояжера – таким чином отримаємо відсортований масив, який буде містити вартості турів в порядку їх зростання. Тобто першим елементом масиву TourCost буде елемент TourCostk вартість якого буде найменшою з поміж усіх елементів масиву. Також слід зауважити. що даний масив повинен бути фіксованого розміру, так як в результаті схрещування будемо отримувати нові батьківські та дочірні хромосоми, а відповідно їх кількість буде перевищувати розмір масиву, то доцільно ввести деяку під функцію сортування, яка буде відповідати за порівняння найкращих генів. Для кращого розуміння розглянемо наприклад ситуацію при якій будемо мати 6 хромосом, припустимо. що в результаті схрещування отримаємо вже 10 хромосом, проте в кінцевому варіанті повинні мати ті ж 6 хромосом з мінімальною вартістю шляху (туру) [3]. Щодо типів даних. які будемо використовувати, то вони будуть цілими значеннями, тому і відповідні структури в програмній реалізації також будуть цілочисельні.
3.2 Розробка оціночної функції для розв’язання задачі комівояжера за допомогою генетичного алгоритму Суть генетичного алгоритму полягає в наступному - нехай на деякому кроці t є популяція G(t), що складається з N рядків. Для популяції вводиться поняття середньої цінності популяції Fср (G(t)):
Аналогічно для підпопуляції GH(t), що задовольняє схемі H, вводиться поняття середньої цінності під популяції Fср (GH(t)):
Генетичний алгоритм здійснює перехід від популяції G(t) до популяції G(t+1) таким чином, щоб середня цінність складових її рядків збільшувалася, причому кількість нових рядків у популяції дорівнює KN, де K - коефіцієнт новизни. Якщо K<1, то в новій популяції зберігаються деякі рядки зі старої, а якщо K=1, то популяція піддасться повному відновленню. Генетичний алгоритм включає три операції: - відтворення; - схрещування; - мутація. Відтворення представляє собою процес вибору K*NN рядків популяції G(t) для подальших генетичних операцій. Вибір проводиться випадковим чином, причому ймовірність вибору рядка Sit пропорційна її цінності [9]:
Процес вибору повторюється K*NN раз. Передбачувана кількість екземплярів рядка Sit в популяції G(t+1) дорівнює:
Операція відтворення збільшує загальну цінність наступної популяції шляхом збільшення числа найбільш цінних рядків. Нехай в популяції G(t) міститься n(Н, t) рядків, які відповідають схемі H. Тоді в результаті відтворення кількість рядків, які відповідають схемі H в популяції G(t+1) дорівнюватиме n(Н,t+1):
Використовуючи вирази для середньої цінності популяції Fср(G(t)) і пiдпопуляціїFср(GH (t)), можна записати формулу (3.5) у вигляді:
Середня цінність пiдпопуляції, що відповідає схемі H, може бути представлена в наступному вигляді:
де с - деяка величина. Тоді формула (3.6) набуде вигляду:
Припустимо, що величина с при зміні t не змінюється, тоді, починаючи з t=0, отримаємо:
тобто в цьому випадку число представників схеми (рядків популяції G (т), відповідних схемі) змінюється в геометричній прогресії. У загальному випадку можна сказати, що процес зміни представників схеми так само апроксимується геометричною прогресією. Таким чином, в результаті операції відтворення схеми, для яких відповідні підпопуляції мають середню цінність вищу за середню в популяції, збільшують кількість своїх представників. Відтворення оперує з рядками, вже присутніми в даній популяції, і саме по собі не здатне відкривати нові області пошуку. Для цієї мети використовується операція схрещування. Схрещування являє собою процес випадкового обміну значеннями відповідних елементів для довільно сформованих пар рядків. Для цього вибрані елементи на етапі відтворення рядка випадковим чином групуються в пари. Далі кожна пара із заданою вірогідністю Рскр піддається схрещуванню. При схрещуванні відбувається випадковий вибір позиції роздільника d (d = 1, 2,..., l-1, де L - довжина рядка). Потім значення перших d елементів першого рядка записуються у відповідні елементи другого, а значення перших d елементів другого рядка - до відповідних елементів першого. В результаті отримуємо два нових рядки, кожен з яких є комбінацією частин двох батьківських рядків. Операція схрещування утворює нові рядки шляхом деякої комбінації значень елементів найбільш цінних в популяції G(t) рядків. Отримані в результаті рядки можуть перевершувати за цінністю батьківські рядки. Розглянемо деяку схему (cхемою в генетичному алгоритмі називають опис деякої підмножини рядків) H=(h1,h2,...,hm ), для якої визначимо порядок о(Н) - число фіксованих позицій схеми і визначальну довжину d(Н) - відстань (число позицій) між першою і останньою фіксованими позиціями. Припустимо, що до операції схрещування рядок S був представником схеми H, тобто S
Врахуємо, що схрещування відбувається з імовірністю Pc, а також те, що навіть якщо позиція роздільника опиниться між фіксованими позиціями схеми, рядок S1 може бути представником схеми H, якщо даний рядок був отриманий схрещуванням двох представників схеми H. Тоді ймовірність Рs,1 того, що рядок S1 є представником схеми H, визначається виразом [9]:
Вважаючи незалежність операцій відтворення і схрещування, оцінимо сукупний ефект від цих операцій, тобто число представників схеми H в популяції G(t+1):
Так як відкриття нових областей пошуку в операції схрещування відбувається лише шляхом перегруповування наявних в популяції комбінацій символів, то при використанні тільки цієї операції деякі потенційно оптимальні області можуть залишатися не розглянутими. Для запобігання подібних ситуацій застосовується операція мутації. Мутація являє собою процес випадкової зміни значень елементів рядка. Для цього рядки, що вийшли на етапі схрещування, проглядаються поелементно, і кожен елемент із заданою вірогідністю мутації Pмут може мутувати, тобто змінити значення на будь-який випадково обраний символ, допустимий для даної позиції. Операція мутації дозволяє знаходити нові комбінації ознак, що збільшують цінність рядків популяції. Припустимо, що до мутації рядок S1був представником схеми H, тобтоS1 Враховуючи, що мутація відбувається з імовірністю Pмут, ймовірність ps2 того, що рядок S2 є представником схеми H, визначається виразом:
де о(Н) - число фіксованих позицій схеми H [10]. Вважаючи незалежність операцій відтворення, схрещування і мутації оцінимо сукупний ефект від цих операцій, тобто число представників схеми H в популяції G (t +1):
Так як, при малих значеннях pm приблизно можна вважати,
то вираз (3.14) можна записати у вигляді:
або
Таким чином, схеми, у яких мала визначальна довжина та порядок, і для яких відповідна підпопуляція має середню цінність, що перевищує середню цінність популяції, експонтенціально збільшують число представників у наступних поколіннях [9]. Наведемо значення оціночної функції для розв'язку задачі комівояжера (рис. 3.2) з наступними параметрами генетичного алгоритму: - кількість ітерацій – 50; - розмір популяції – 200; - ймовірність мутації – 0,2, де матриця вартостей переїзду між містами має вигляд, який зображений на рисунку 3.1.
Рисунок 3.1 - Матриця вартостей переїзду між містами
Рисунок 3.2 – Розв’язок задачі комівояжера
В даному випадку найкраще значення оціночної функції всіх особин серед усіх популяцій становить 106, а середнє значення по оціночним функціям після 50 виконаних ітерацій – 161,1.
|

 . (3.1)
. (3.1) . (3.2)
. (3.2) . (3.3)
. (3.3) . (3.4)
. (3.4)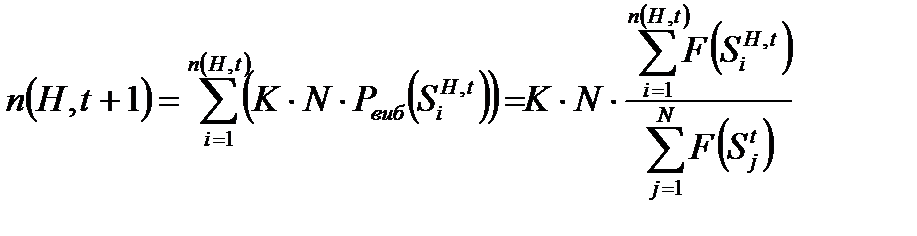 . (3.5)
. (3.5) . (3.6)
. (3.6) , (3.7)
, (3.7) . (3.8)
. (3.8) , (3.9)
, (3.9) UH. Припустимо, що рядок S1отриманий з рядка S в результаті схрещування. Рядок S1 буде представником схеми H в тому випадку, якщо позиція роздільник при схрещуванні не розташовувалася між фіксованими позиціями схеми. Ймовірність того, що позиція роздільника опиниться між фіксованими позиціями схеми, дорівнює:
UH. Припустимо, що рядок S1отриманий з рядка S в результаті схрещування. Рядок S1 буде представником схеми H в тому випадку, якщо позиція роздільник при схрещуванні не розташовувалася між фіксованими позиціями схеми. Ймовірність того, що позиція роздільника опиниться між фіксованими позиціями схеми, дорівнює: . (3.10)
. (3.10) . (3.11)
. (3.11) . (3.12)
. (3.12) , (3.13)
, (3.13) . (3.14)
. (3.14) , (3.15)
, (3.15) , (3.16)
, (3.16) . (3.17)
. (3.17)




