Теоретические сведения. Постановка задачи. Требуется найти решение уравнения вида f(x)=0
Постановка задачи. Требуется найти решение уравнения вида f(x)=0. Решением является такое значение x=x*, при котором исходное уравнение обращается в тождество. Численное решение нелинейного уравнения состоит из двух этапов: 1) отделение (изолирование) корня; На этапе изолирования корня определяется отрезок [a;b], которому принадлежит корень и на котором он единственный. Изолировать корни можно различными способами: табулированием, графически. Для графического изолирования корней уравнение f(x)=0 заменяют равносильным уравнением φ(x)=ψ(x) и строят графики функций y1=φ(x) и y2=ψ(x). Абсциссы точек пересечения этих графиков дают приближённые значения искомых корней. Единственность корня проверяется выполнением теоремы Коши: если функция 2) уточнение значения корня. Рассмотрим общие принципы решения уравнений итерационными методами. Дано уравнение f(x)=0 с изолированным корнем Преобразуя уравнение 1. в методе простой итерации 2. в методе Ньютона 3. в методе хорд (секущих) Итерационный процесс заканчиваем при выполнении условия Погрешность методов определяется по следующим формулам:
|

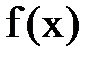 непрерывна и дифференцируема на отрезке [a;b] и на концах этого отрезка имеет значения разных знаков, а первая и вторая производные сохраняют знак на этом отрезке, то внутри этого отрезка существует корень и он единственный.
непрерывна и дифференцируема на отрезке [a;b] и на концах этого отрезка имеет значения разных знаков, а первая и вторая производные сохраняют знак на этом отрезке, то внутри этого отрезка существует корень и он единственный.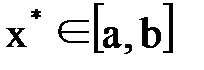 . Преобразуем уравнение к виду
. Преобразуем уравнение к виду  . Итерационный процесс состоит в последовательном уточнении начального приближения
. Итерационный процесс состоит в последовательном уточнении начального приближения  :
:  ,
,  ,
, 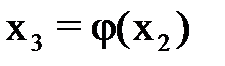 , …
, …  . Каждый такой шаг называется итерацией. В результате итераций находим последовательность приближённых значений корня
. Каждый такой шаг называется итерацией. В результате итераций находим последовательность приближённых значений корня  .
. к виду, удобному для итераций, получим уравнение вида
к виду, удобному для итераций, получим уравнение вида  при
при 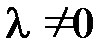 . В зависимости от значения λ различают и методы решения уравнений:
. В зависимости от значения λ различают и методы решения уравнений: , где
, где 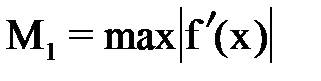 при
при 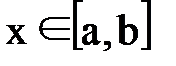 . Итерационная формула имеет вид:
. Итерационная формула имеет вид:  , где
, где 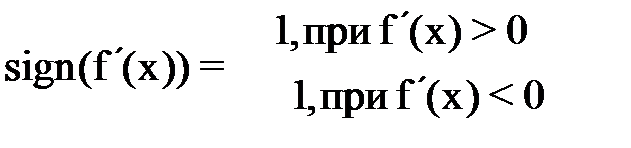 . Метод сходится при любом начальном приближении
. Метод сходится при любом начальном приближении 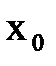 .
.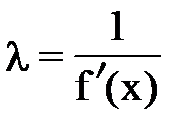 . Итерационная последовательность
. Итерационная последовательность  сходится при выборе начального приближения из условия
сходится при выборе начального приближения из условия  .
. . Итерационная последовательность
. Итерационная последовательность  сходится при выборе начального приближения из условия
сходится при выборе начального приближения из условия 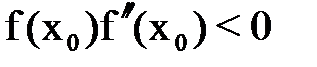 . Через
. Через  обозначены координата и значение функции в неподвижном конце промежутка.
обозначены координата и значение функции в неподвижном конце промежутка. , где
, где  - заданная точность приближения.
- заданная точность приближения.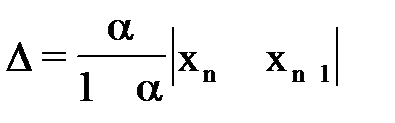 - метода простой итерации, где
- метода простой итерации, где 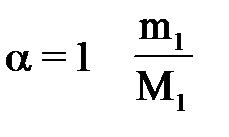 ;
;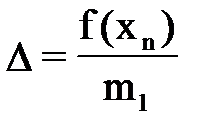 - методов Ньютона и хорд, где
- методов Ньютона и хорд, где 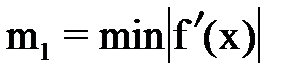 на отрезке
на отрезке 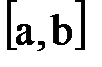 .
.


